Основные следствия из преобразований Лоренца

Следствия из преобразований Лоренца.

Самым неожиданным следствием теории относительности является зависимость времени от системы отсчета.

Длительность событий в разных системах отсчета. Пусть в некоторой точке , покоящейся относительно подвижной системы , происходит событие, длительность которого = - , где и - начальный и конечный промежутки времени. C помощью формул (7.4) получим, что длительность этого же события в неподвижной системе отсчетаK равна

или

(7.5)

Из последнего равенства следует, что , т.е. для подвижной системы отсчета событие будет происходить за меньший промежуток времени. Следовательно, для подвижной системы отсчета время идет медленнее. Этот удивительный результат можно понять, если придумать специальные часы, в которых роль маятника играет световой сигнал, бегающий между двумя параллельными зеркалами, находящимися на расстоянииL. Период таких часов для системы отсчета, в которой они покоятся =2L /с. Если эти часы движутся со скоростьюvoвдоль осиx(рис. 7.2), то для неподвижного наблюдателя траектория движения луча выглядит в виде зигзага и расстояние, пройденное светом за период часовt, будет более длинным, его квадрат равен4L2+ t2 = с2t2. ИсключаяL из двух последних равенств, легко получить выражение (7.5)t = /(1-- b 2)0,5. Если космонавт улетит от Земли со скоростью, близкой к скорости света (например,b 2 = 1 - 10-4), и вернется обратно через год, то по земным часам полет продлится 100 лет. Космонавт возвратится на Землю в сто раз более молодым, чем его брат-близнец. Данный результат мысленного эксперимента кажется неправильной интерпретацией преобразований Лоренца, так как, если за неподвижную систему отсчета считать движущийся корабль, то его близнец на Земле удаляется с такой же скоростью, и его время как бы замедлится по сравнению с часами на корабле. Однако эти две системы – не равнозначны, космонавт на корабле должен ускоряться и замедляться, чтобы вернуться на Землю. Поэтому система отсчета, связанная с кораблем ‑ неинерциальна. Получается, что причина замедления физических процессов связана с тем, что космонавт при путешествии подвергался дополнительным механическим перегрузкам. Детальный расчет, выходящий за рамки специальной теории относительности, показывает, что часы, движущиеся с ускорением, идут медленнее, поэтому при возвращении отстанут именно они.

Эффект замедления хода часов получил экспериментальное подтверждение при исследовании частиц m-мезонов, образующихся в космических лучах. Среднее время жизни неподвижныхm-мезонов составляет 2 10-6с. Казалось бы, что двигаясь со скоростью светаm-мезоны могут пройти расстояние 600м. Однакоm-мезоны проходят расстояние 20-30кми достигают земной поверхности, т.е. для земного наблюдателя время жизниm-мезонов оказывается гораздо большим.

Одновременность событий в разных системах отсчета. Пусть в подвижной системе в точках с координатами и происходят одновременно два события в момент времени = =b. Согласно формулам (7.4) в системеKэтим событиям будут соответствовать координатыt1= (b + vo /c2)/(1- - b 2)0,5 иt2 = (b + vo /c2)/(1-b 2)0,5. Из написанных формул видно, что если события в системеK пространственно разобщены( ¹ ), они не будут происходить одновременно. Например, при > получимt1>t2, т.е. событие в точке1для неподвижной системы отсчета произойдет раньше, хотя для подвижной системы эти события одновременны.

Длина тел в разных системах отсчета. Из преобразований (7.4) следует, что при движении тел их размеры по осямx иy не изменяются. Пусть в системеK покоится стержень, параллельный осиx. Длина его, измеренная в этой системе, равнаl = x2 - x1, гдеx1 иx2- координаты обоих концов стержня в системеK. Используя преобразования Лоренца (7.4), выразим длину стержня в следующем видеl = ( +vo 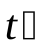)/(1- b 2)0,5 - ( + +vo 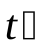)/(1- b 2)0,5 = ( - )/(1-b 2)0,5, где и - координаты концов стержня, измеренные в подвижной системе в один и тот же момент времени 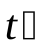. Длина стержня в системе равна = - . Окончательно получимl = /(1- b 2)0,5 или =l(1- b 2)0,5. Отсюда следуетl > . Длинуlназываютсобственной длинойстержня в той системе отсчета, в которой он покоится.Это наибольшая длина стержня. Если предмет начинает двигаться, его размеры в направлении осиxсокращаются пропорционально(1- b 2)0,5. Например, если неподвижное тело является шаром, то при движении шар сжимается вдоль осиx, приобретая форму эллипсоида вращения.

Релятивистский закон сложения скоростей. Пусть опять система движется относительно системыKсо скоростьюvoвдоль осиx. Пустьvx = dx/dt есть компонента скорости некоторой частицы в системеK, а = - компонента скорости ее в системе . Дифференцируя формулы (7.4), получим

; dy = d ; dz = dz’; .

Разделив первые три равенства на четвертое и учитывая, что b=vo/c, находим

(7.6)

где vx, vy, vz - составляющие скорости частицы в системеK, , , - составляющие скорости частицы в системе 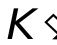. Полученные формулы и определяют преобразование скоростей. Прис® релятивистские формулы переходят в формулы классической механики.

Пусть корабль движется вдоль оси x со скоростью =c / 2 и некоторая частица движется в этом же направлении относительно корабля со скоростью =c / 2.По формулам (7.6) получимvx=4c/5, т.е. по теории относительности1/2и1/2 дают не1, а 4/5.

Возьмем предельный случай. Положим, что человек на борту корабля наблюдает, распространение света вдоль оси x, т.е. =с. Тогда по формулам (8.6) получимvx=(с + )/(1 + c/c2) = c. Итак, скорость света для неподвижного наблюдателя опять равна скорости света.