Волновая функция и уравнение Шредингера. Статический смысл волновой функции

Уравнение учитывающее волновые и корпускулярные свойства частицы было получено Шредингером в 1926г.

Шредингер сопоставил движение частицы на комплексную функцию координат и времени, которая называется функцией, эта функция является решением уравнения Шредингера:

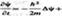
, где 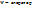Лапласа, который можно

расписать: 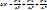; ; 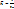U-потенциальная энергия частицы 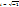; Где - функция координат и времени.

В квантовой физикенельзя точно предсказатькакие либо события, а можно говорить только о вероятностиданного события, вероятность событий и определяет .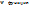

1) Вероятность нахождения микрочастицы в объеме dV в момент времени Т: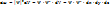

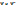-сопряженные функции.

2) Плотность вероятностей нахождения частицы в единице объема:

.

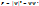3) Волновая функция должна удовлетворять условию:

где 3 интеграла расчитываются по всему объему, где может находится частица.

Данное условие означает, что пробывание частицы – достоверное событие с вероятностью 1