Уравнение Шредингера для стационарных состояний. Условия, налагаемые на волновую функцию. Нормировка волновой функции

Для некоторых практических задач потенциальная энергия частицы не зависит от времени. В этом случае волновую функцию можно представить как произведение

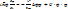т.к. зависит только от времени, то 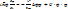разделим на 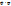получим:

Левая часть равенства зависит только от времени, правая только от координат, это равенство справедливо только если обе части = const, такой константоя является полная энергия частицы Е.

Рассмотрим правую часть данного равенства: , преобразуем: - уравнение для стационарного состояния.

Рассмотрим левую часть уравнения Шредингера: ; ;

разделим переменные , проинтегрируем полученное уравнение:

воспользуясь математическими преобразованиями:

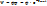
В этом случае вероятность нахождения частицы можно определить:

, либо после преобразований:

– данная вероятность не зависит от времени, данное уравнение, характеризующее микрочастицы, получило название – стационарное состояние частицы.

Обычно требуют, чтобы волновая функция была определена и непрерывна (бесконечное число раз дифференцируема) во всем пространстве, а также чтобы она была однозначной. Допустимым является один вид неоднозначности волновых функций —неоднозначность знака «+/».

Волновая функция по своему смыслу должна удовлетворять так называемому условию нормировки, например, в координатном представлении имеющему вид:

Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо во всём пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении.