Уравнение Шредингера. Волновая ф-ция и ее физический смысл

Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике. Установлено Эрвином Шрёдингером в 1926 году.

Наиболее общая форма уравнения Шрёдингера — это форма, включающая зависимость от времени:

Зависимое от времени уравнение (общий случай)

, где — гамильтониан.

В квантовой физике вводится комплекснозначная функция 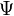, описывающая чистое состояние объекта, которая называется волновой функцией

Пусть волновая функция задана в n-мерном конфигурационном пространстве, тогда в каждой точке с координатами , в определенный момент времени t она будет иметь вид . В таком случае уравнение Шрёдингера запишется в виде:

где , — постоянная Планка; — масса частицы, — потенциальная энергия в точке в момент времени , — оператор Лапласа

Волнова́я фу́нкция, или пси-функция — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

где — координатный базисный вектор, а — волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

В координатном представлении волновая функция зависит от координат системы. Физический смысл приписывается квадрату её модуля , который интерпретируется как плотность вероятности 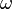обнаружить систему в положении, описываемом координатами в момент времени :

.

Тогда в заданном квантовом состоянии системы, описываемом волновой функцией , можно рассчитать вероятность того, что частица будет обнаружена в любой области конфигурационного пространства конечного объема :

2.Вязкая жидкость. Формула Стокса. Формула Пуазейля.

Вязкая жидкость (Ньютоновская жидкость) - это жидкость в которой возникает трение во время движения

Простое уравнение, описывающее силы вязкости в ньютоновской жидкости, во многом определяющие ее поведение, основано на сдвиговом течении:

,

где:

• — касательное напряжение, вызываемое жидкостью, Па;
• — динамический коэффициент вязкости — коэффициент пропорциональности, Па·с;
• — производная скорости в направлении, перпендикулярном направлению сдвига, с⁻¹.

Закон Стокса описывает силу трения при движении в вязкой жидкости.

Где:

· — сила трения, так же называемая силой Стокса,

· — радиус сферического объекта,

· — динамическая вязкость жидкости,

· — скорость частицы.

Согласно Пуайзелю, объем вытекаемой вязкой жидкости через капилляр равен:

· V— объем жидкости,

· R - радиус капилляра,

· L — длина капилляра,

· — динамическая вязкость жидкости,

· p_1-p₂— перепад давления,

· t - время движения

Билет №22.