Работа газа при изменении объема газа

Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находящийся под поршнем в цилиндрическом сосуде (рис. 78). Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то производит над ним работу

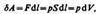
где S — площадь поршня, Sdl=dV— изменение объема системы Таким образом,

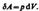(52.1)

Полную работу А, совершаемую газом при изменении его объема от V1 до V2, найдем интегрированием формулы (52.1):

Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (52.2) справедливо при любых изменениях объема твердых, жидких и газообразных тел. Количество теплоты. Коли́чество теплоты́ — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин.Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние. Первый закон термодинамики Количество теплоты, сообщённое газу, идёт на приращение внутренней энергии газа и на совершение газом работы над внешними телами. - первое начало термодинамики. Идеальный газ Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. 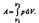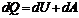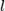Вывод основного уравнения молекулярно-кинетической теорииПусть имеется кубический сосуд с ребром длиной и одна частица массой m в нём. Обозначим скорость движения тогда перед столкновением со стенкой сосуда импульс частицы равен а после — поэтому стенке передается импульс 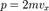. Время, через которое частица сталкивается с одной и той же стенкой, равно 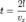Отсюда следует: 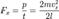Так как давление 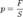следовательно сила 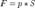Подставив, получим: 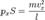Преобразовав: 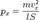Так как рассматривается кубический сосуд, то Отсюда: 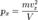Соответственно, 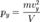и 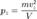Таким образом, для большого числа частиц верно следующее: 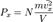аналогично для осей y и z. Поскольку 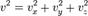то 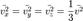Это следует из того, что все направления движения молекул в хаотичной среде равновероятны. Отсюда 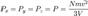или 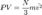Пусть 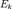— среднее значение кинетической энергии всех молекул, тогда: 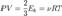откуда 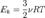Для одного моля выражение примет вид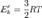 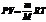Молекулярно-кинетическое толкование абсолютной температуры Абсолютная температура – есть величина, пропорциональная средней энергии поступательного движения молекул. Уравнение Менделеева-Клапейрона М - масса 1 моля газа, R = 8,31 - универсальная газовая постоянная. Законы идеальных газов 1. Закон Бойля – Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная: pV=const при T=const, m=const (7) Процесс, протекающий при постоянной температуре, называется изотермическим. Кривая, изображающая зависимость между величинами p и V, характеризующими свойства вещества при постоянной температуре, называется изотермой. Изотермы представляют собой гиперболы, расположенные тем выше, чем выше температура, при которой происходит процесс (рис. 1). Рис. 1. Зависимость давления идеального газа от объема при постоянной температуре 2. Закон Гей-Люссака: объем данной массы газа при постоянном давлении изменяется с температурой линейно:   V=V0(1+αt) при p=const, m=const (8) Здесь t - температура по шкале Цельсия, V0 - объем газа при 0 oС, α=(1/273) K-1 - температурный коэффициент объемного расширения газа. Процесс, протекающий при постоянном давлении и неизменной массе газа, называется изобарным. В ходе изобарного процесса для газа данной массы отношение объема к температуре постоянно: 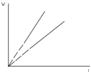V/T=const.На диаграмме в координатах (V,t) этот процесс изображается прямой, называемой изобарой (рис. 2). Рис. 2. Зависимость объема идеального газа от температуры при постоянном давлении 3. Закон Шарля: давление данной массы газа при постоянном объеме изменяется линейно с температурой: p=p0(1+αt) при p=const, m=const (9)   Здесь t - температура по шкале Цельсия, p0 - давление газа при 0 oС, α=(1/273) K-1 - температурный коэффициент объемного расширения газа. Процесс, протекающий при постоянном объеме и неизменной массе газа, называется изохорным. В ходе изохорного процесса для газа данной массы отношение давления к температуре постоянно: P/T=const. На диаграмме в координатах этот процесс изображается прямой, называемой изохорой (рис. 3). Рис. 3. Зависимость давления идеального газа от температуры при постоянном объеме Вводя в формулах (8) и (9) термодинамическую температуру T, законам Гей-Люссака и Шарля можно придать более удобный вид: V=V0(1+αt)=V0[1+α(T-1/α)]=V0αT (10) p=p0(1+αt)=p0[1+α(T-1/α)]=p0αT (11) Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. Так, при нормальных условиях один моль любого газа занимает объем 22,4 м-3. При одинаковых температуре и давлении любой газ содержит в единице объема одинаковое количество молекул. При нормальных условиях в 1 м3 любого газа содержится число частиц, называемое числом Лошмидта: NL=2,68·1025 м-3. Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений p1,p2,...,pn входящих в нее газов: p=p1+p2+....+pn Парциальное давление – давление, которое создавал бы газ, входящий в состав газовой смеси, если бы он занимал объем, равный объему смеси при той же температуре. Число степеней свободы молекул Числом степеней свободы материального объекта называют число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета. Например, положение материальной точки в пространстве определяется тремя координатами x, y, z, следовательно, материальная точка обладает тремя степенями свободы. 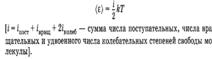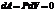Средняя энергия молекул 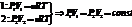Применение первого закона термодинамики при изохорическом, изобарическом, изотермических процессах 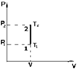Этот закон является частным случаем уравнения состояния идеального газа: PV = nRT Изохорический процесс   --закон Ширля

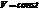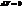Так как то и,т.е

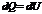
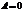т.е первое начало термодинамики для изохорического процесса.

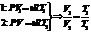Изобарический процесс зак. Гей-Люссака

 

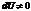
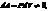Работа, совершаемая газом, приращение внутренней энергии газа тоже не равно нулю

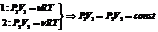первое начало термодинамики для изобарического процесса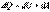

 

 

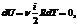Так как T = const, то т. е. dU = 0

т. е. dU = 0 dQ = dA - первое начало термодинамики при изотермическом процессе