2018-01-08
613
Как уже отмечалось, в нелинейных АСР наблюдаются устойчивые периодические колебания постоянной амплитуды и частоты, так называемые автоколебания. Причем автоколебания могут сохраняться даже при значительных изменениях параметров системы. Практика показала, что во многих случаях колебания регулируемой величины (рис. 3) близки к гармоническим.
 |
Близость автоколебаний к гармоническим позволяет использовать для определения их параметров – амплитуды A и частоты w0 – метод гармонической линеаризации. В основе метода лежит предположение, что линейная часть системы является фильтром низких частот (гипотеза фильтра). Определим условия, при которых автоколебания в системе могут быть близки гармоническим. Структурная схема АСР приведена на рис. 3. Прямой путь передачи задающего воздействия содержит, последовательно соединенные нелинейный элемент и передаточную функцию линейной части.
Предположим, что сигнал задания 
величина постоянная, для простоты примем его равным нулю. А сигнал ошибки 
(рис 3) является гармоническим:
|
|
|
(1)
Выходной сигнал нелинейного элемента 
как всякий периодический сигнал – на рисунке 3 это прямоугольные колебания – может быть представлен в виде суммы гармоник ряда Фурье.
(2)
Для простоты будем считать, что постоянная составляющая 
равна нулю, что характерно для астатических систем.
Допустим, что линейная часть системы является фильтром низких частот (рис. 4) и пропускает только первую гармонику с частотой w0. Вторая с частотой 2w0 и более высокие гармоники отфильтровываются линейной частью. В этом случае на выходе линейной части будет существовать практически только первая гармоника, а влиянием высших гармоник можно пренебречь
. (3)
Таким образом, если линейная часть системы является фильтром низких частот, а частота автоколебаний w0 удовлетворяет условиям
, 
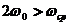(4)
то автоколебания в системе можно считать гармоническими.
Предположение, что линейная часть системы является фильтром низких частот, называется гипотезой фильтра. Гипотеза фильтра выполняется всегда, если разность степеней полиномов знаменателя и числителя передаточной функции линейной части
(5)
не меньше двух
. (6)
Условие (6) выполняется для многих реальных систем. Примером могут служить апериодическое звено второго порядка и реальное интегрирующее
,
. (7)
Таким образом, при выполнении гипотезы фильтра в расчетах рассматривается только первая гармоника периодических колебаний на выходе нелинейного элемента. В режиме автоколебаний выполняется процедура гармоническая линеаризация нелинейного элемента. Нелинейный элемент заменяется эквивалентным линейным с комплексным коэффициентом усиления (описывающей функцией) 
, зависящим от амплитуды входного гармонического сигнала:
|
|
|
, (8)
где 
и 
– действительная и мнимая части ,
– аргумент ,
– модуль .
В общем случае зависит как от амплитуды так и частоты автоколебаний и постоянной составляющей 
. Физически комплексный коэффициент усиления нелинейного элемента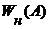 
, чаще называемый коэффициентом гармонической линеаризации, есть комплексный коэффициент усиления нелинейного элемента по первой гармонике. Модуль коэффициента гармонической линеаризации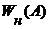
(9)
численно равен отношению амплитуды первой гармоники на выходе нелинейного элемента к амплитуде входного гармонического сигнала.
Аргумент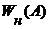
(10)
характеризует сдвиг по фазе между первой гармоникой выходных колебаний и входным гармоническим сигналом. Для однозначных нелинейностей, таких как, например, на рис. 2,а и 2,б, 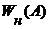действительное выражение и
.
Для неоднозначных нелинейностей, рис. 2,в определяется по формуле
, (11)
где S – площадь петли гистерезиса.
В общем случае и вычисляются по формулам
,
, 
(12)
где 
, 
– нелинейная функция (характеристика нелинейного элемента).
С учетом вышеизложенного, при исследовании автоколебаний, близких к гармоническим, нелинейная АСР (рис. 3) заменяется эквивалентной линейной (рис. 5).
|
|
|
|
|
|
|
Выходной сигнал нелинейного элемента на рис. 5 обозначен как 
, это подчеркивает, что нелинейный элемент генерирует только первую гармонику колебаний. Формулы для коэффициентов гармонической линеаризации для типовых нелинейностей можно найти в литературе, например, в [1,2,5]. В таблице приложения В приведены характеристики исследуемых релейных элементов, формулы для 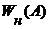и их годографы. Там же приведены формулы и годографы для обратного коэффициента гармонической линеаризации 
, определяемого выражением
, (13)
где 
и 
действительная и мнимая часть 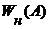. Годографы 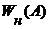и строятся в координатах , и 
, 
соответственно.
Запишем теперь условия существования автоколебаний. Система на рис. 5 эквивалентна линейной. В линейной системе существуют незатухающие колебания, если она находится на границе устойчивости. Воспользуемся условием границы устойчивости по критерию Найквиста:
. (14)
Уравнение (14) есть условие существования автоколебаний, близких к гармоническим. Если существуют действительные положительные решения А и w0 уравнения (14), то в нелинейной АСР существуют автоколебания близкие к гармоническим. В противном случае автоколебания отсутствуют или не являются гармоническими. Уравнение (14) распадается на два – относительно действительной и мнимой части:
;
(15)
или
;
. (16)
Поделив обе части уравнения (14) на 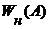и принимая во внимание формулу (13), получим условие существования автоколебаний в форме Гольдфарба Л.С.:
. (17)
Уравнение (17) также распадается на два:
,
(18)
и в некоторых случаях ими удобнее пользоваться для определения параметров автоколебаний.
Гольдфарб предложил графоаналитический метод решения системы (17) и определения устойчивости автоколебаний.
В координатах 
, и 
, строятся годографы 
и (рис. 6). Если годографы пересекаются, то автоколебания существуют. Параметры автоколебаний – А и w0 определяются в точках пересечения – частота w0 по годографу , амплитуда по годографу . На рис. 6 – две точки пересечения, что указывает на наличие двух предельных циклов.
Для определения устойчивости автоколебаний согласно Гольдфарбу штрихуется левая сторона КЧХ линейной части при движении вдоль КЧХ в направлении возрастания частоты (рис. 6).
 | |||
| |||
|
|
|
Рис. 6
Автоколебания устойчивы, если в точке пересечения годограф нелинейного элемента переходит из незаштрихованной области в заштрихованную при движении в сторону возрастания амплитуды А.
Если переход происходит из заштрихованной области в не- заштрихованную, то автоколебания не устойчивы.
В случае однозначных нелинейностей мнимая часть годографа нелинейного элемента равна нулю. Точка пересечения годографов лежит на вещественной оси, чаще всего, это отрицательная полуось, рис. 7. Система уравнений (18) принимает вид
,
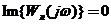. (19)
Частота автоколебаний определяется из второго уравнения системы (19) и для однозначных нелинейностей зависит только от свойств линейной части АСР и не зависит от вида нелинейности. После определения частоты из первого уравнения находится значение , а затем амплитуда автоколебаний.
Для трехпозиционного реле (рис. 7,а) прямой и инверсный коэффициенты гармонической линеаризаци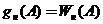и 
и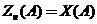 
двузначные функции амплитуды
,
, (20)
имеющие экстремум (максимум)
,
, (21)
при значении амплитуды 
. (22)
Одному значению усиления в общем случае соответствует два значения амплитуды А1 и А2 (рис. 7,а), а обе ветви годографа (рис. 7,б) сливаются и для удобства анализа изображаются как две параллельные ветви. Таким образом, в системе существуют два предельных цикла одинаковой частоты, но различной амплитуды. Устойчивость автоколебаний предлагается оценить по методу Гольдфарба самостоятельно. По рис. 7,а легко проследить влияние коэффициента усиления линейной части Кл на параметры автоколебаний. Уменьшив величину Кл можно добиться срыва автоколебаний, в этом случае годографы и не пересекаются. Этого же эффекта можно добиться, увеличив зону нечувствительности d или уменьшив амплитуду выходного сигнала реле В. Существует некоторое предельное значение Кл, при котором АФХ линейной части касается Ошибка! Ошибка связи. при этом 
, а значение амплитуды равно .
