Щоб поділити добуток на число, досить поділити на це число один із множників і результат помножити на другий множник: 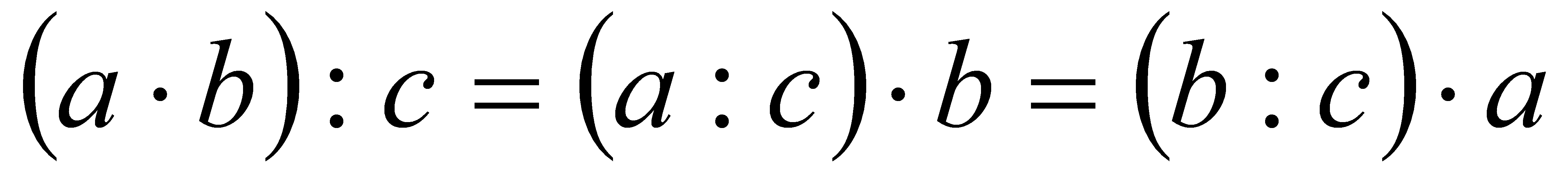 .
.
Доведемо, наприклад, що 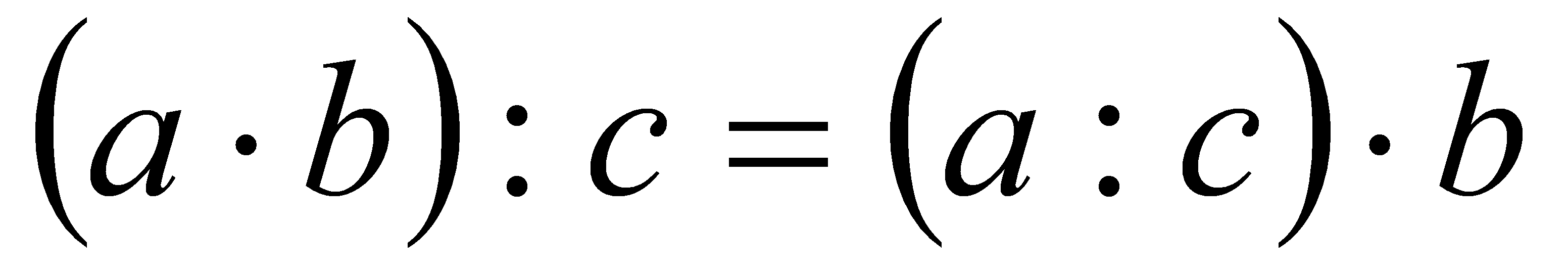 . Якщо ця рівність правильна, то за означенням ділення
. Якщо ця рівність правильна, то за означенням ділення 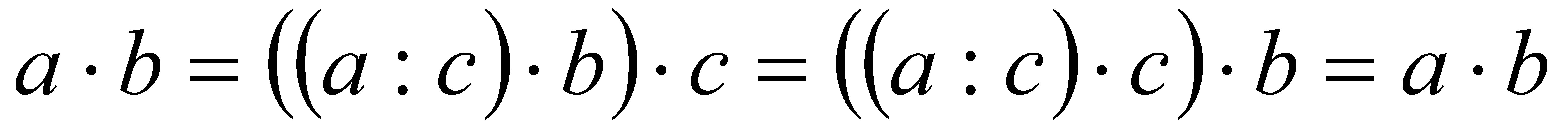 .
.
Правило ділення числа на добуток.
Щоб поділити деяке число на добуток, досить поділити це число на один із множників і знайдену частку поділити на другий множник: 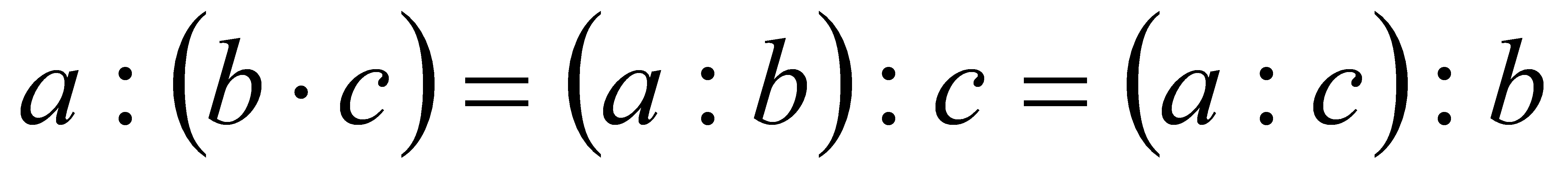 .
.
На цьому правилі ґрунтується послідовне ділення при усних обчисленнях: 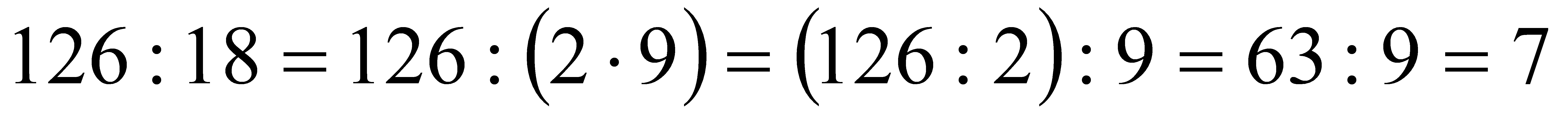 .
.
Ділення з остачею
Ділення одного натурального числа на інше ціле не завжди виконується. Тому розглядають більш загальну дію — ділення з остачею.
Поділити натуральне число 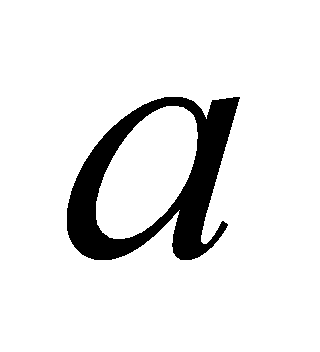 на натуральне число
на натуральне число 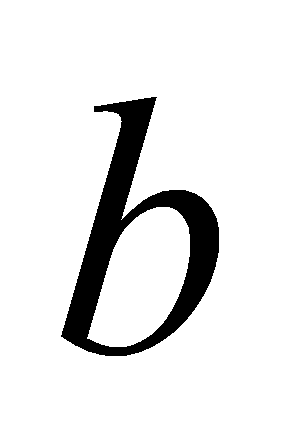 з остачею — означає подати число
з остачею — означає подати число 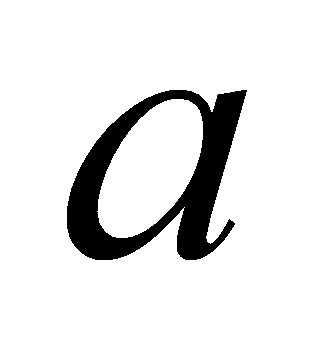 у вигляді
у вигляді 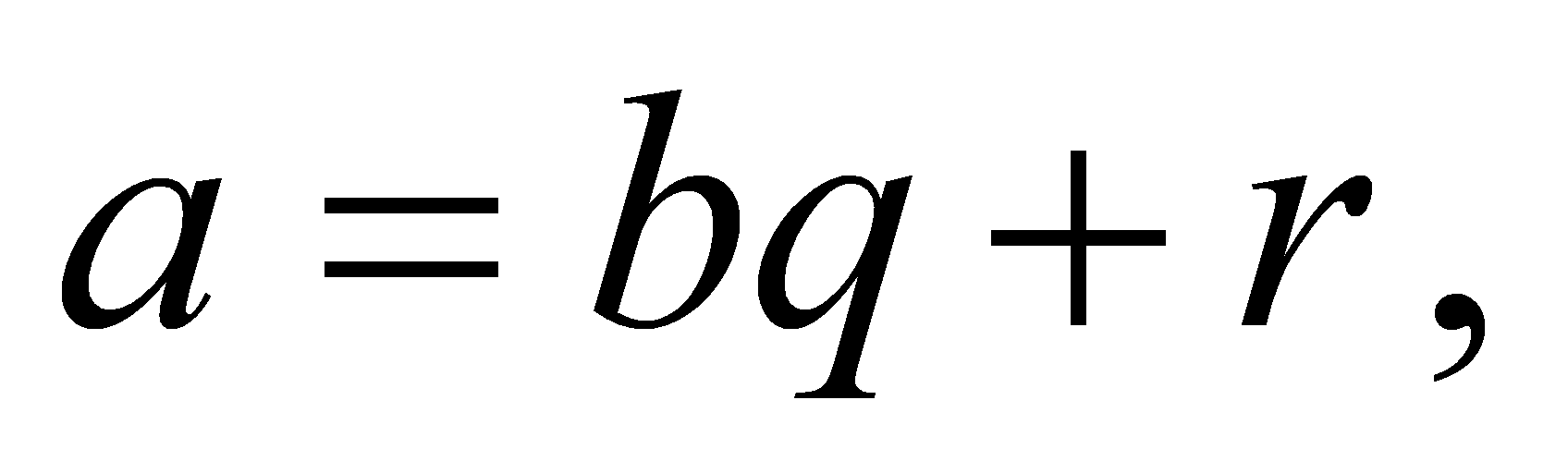 де
де 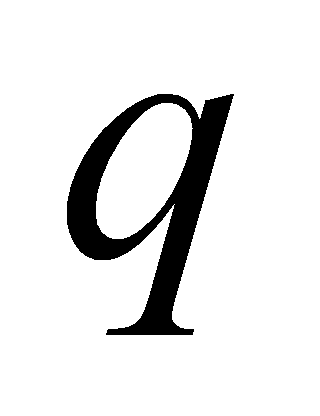 і
і 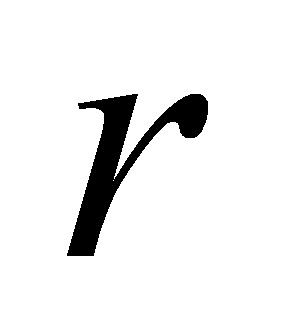 — невід’ємні цілі числа, причому
— невід’ємні цілі числа, причому 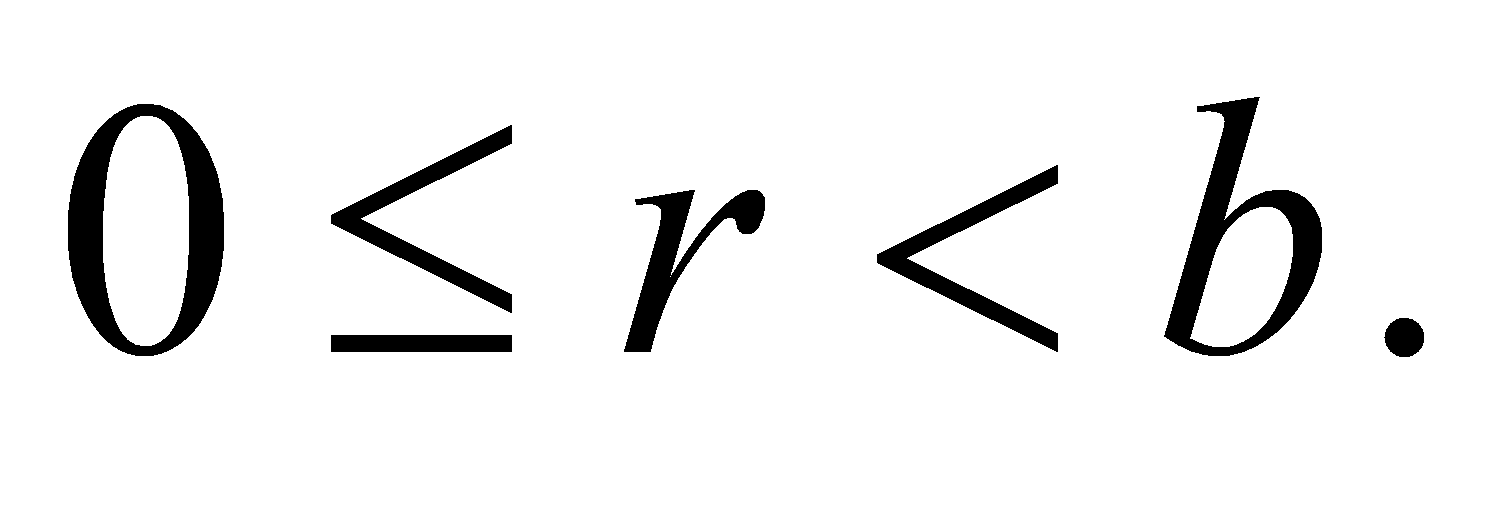 Число
Число 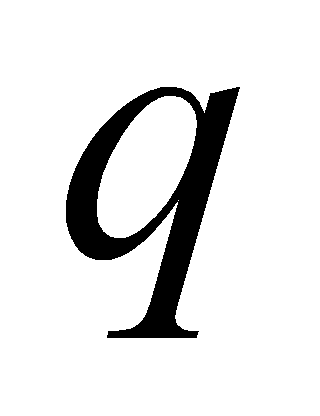 при цьому називається неповною часткою, а число
при цьому називається неповною часткою, а число 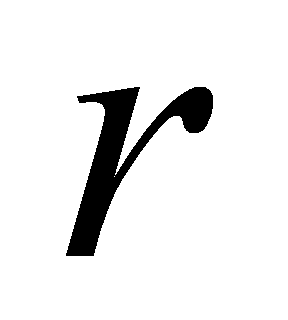 — остачею від ділення
— остачею від ділення 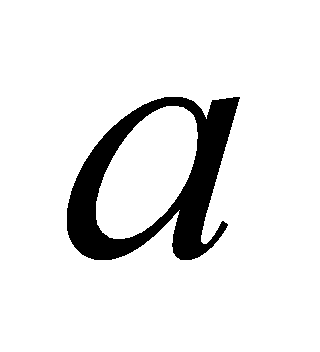 на
на 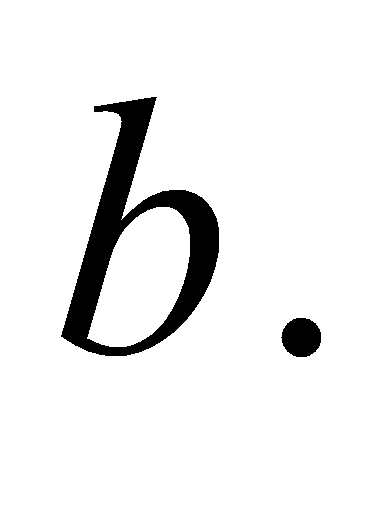 Наприклад, при діленні числа 27 на 6 неповна частка дорівнює 4, а остача
Наприклад, при діленні числа 27 на 6 неповна частка дорівнює 4, а остача 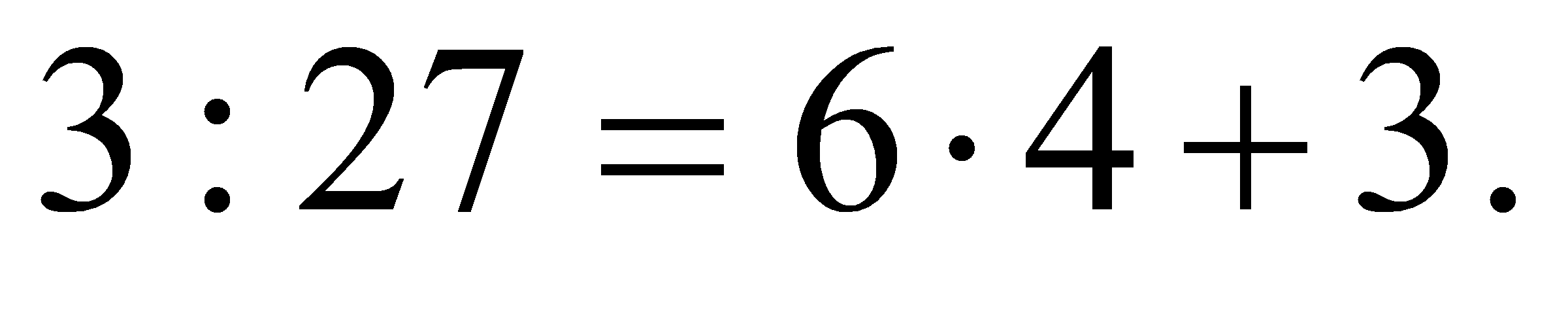 Щоб знайти ділене при діленні з остачею, потрібно неповну частку помножити на дільник і до здобутого добутку додати остачу. Очевидно, що
Щоб знайти ділене при діленні з остачею, потрібно неповну частку помножити на дільник і до здобутого добутку додати остачу. Очевидно, що 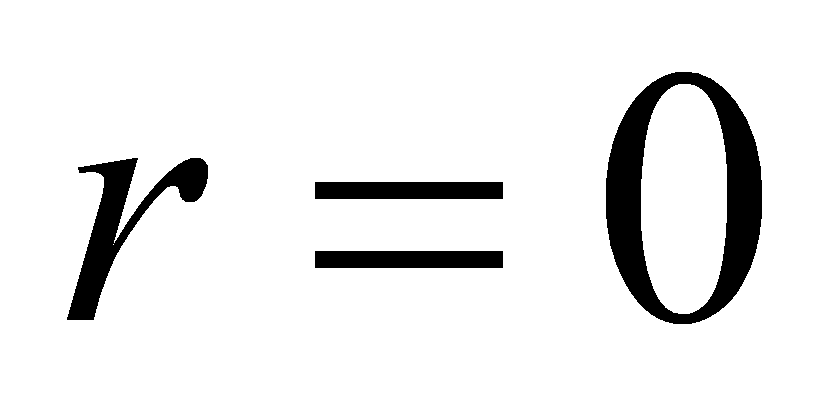 тоді і тільки тоді, коли
тоді і тільки тоді, коли 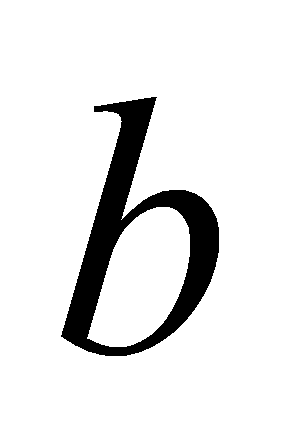 є дільником
є дільником 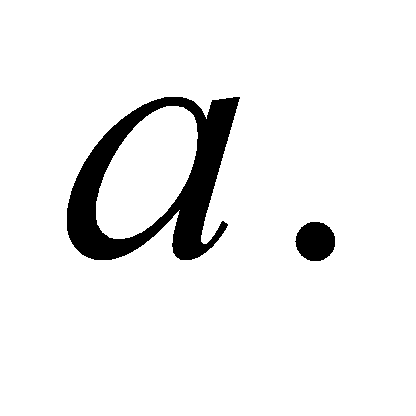 Ділення з остачею завжди виконується, про що свідчить наведена далі теорема (теорема про ділення з остачею).
Ділення з остачею завжди виконується, про що свідчить наведена далі теорема (теорема про ділення з остачею).
Теорема. Для будь-яких натуральних чисел 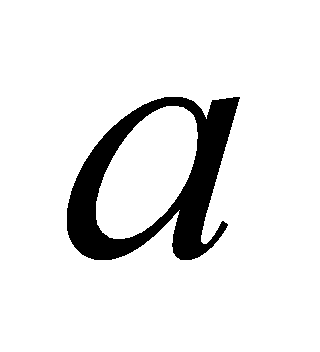 і
і 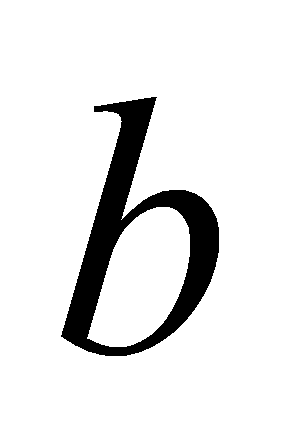 існує єдина пара невід’ємних цілих чисел
існує єдина пара невід’ємних цілих чисел 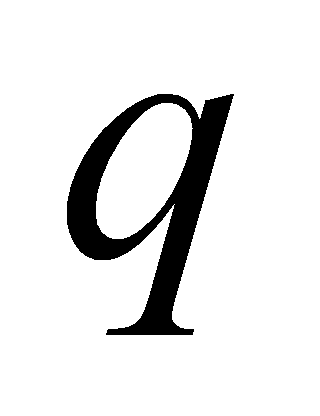 і
і 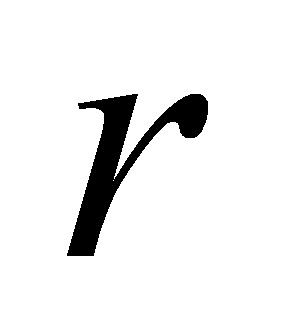 , таких що
, таких що
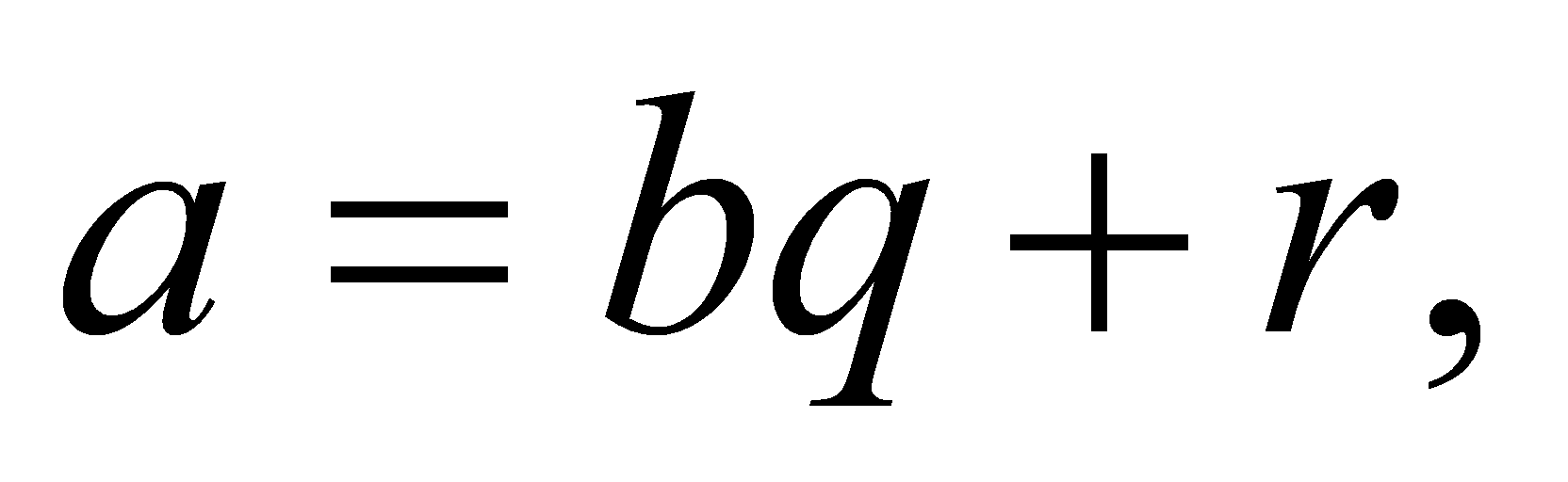
де 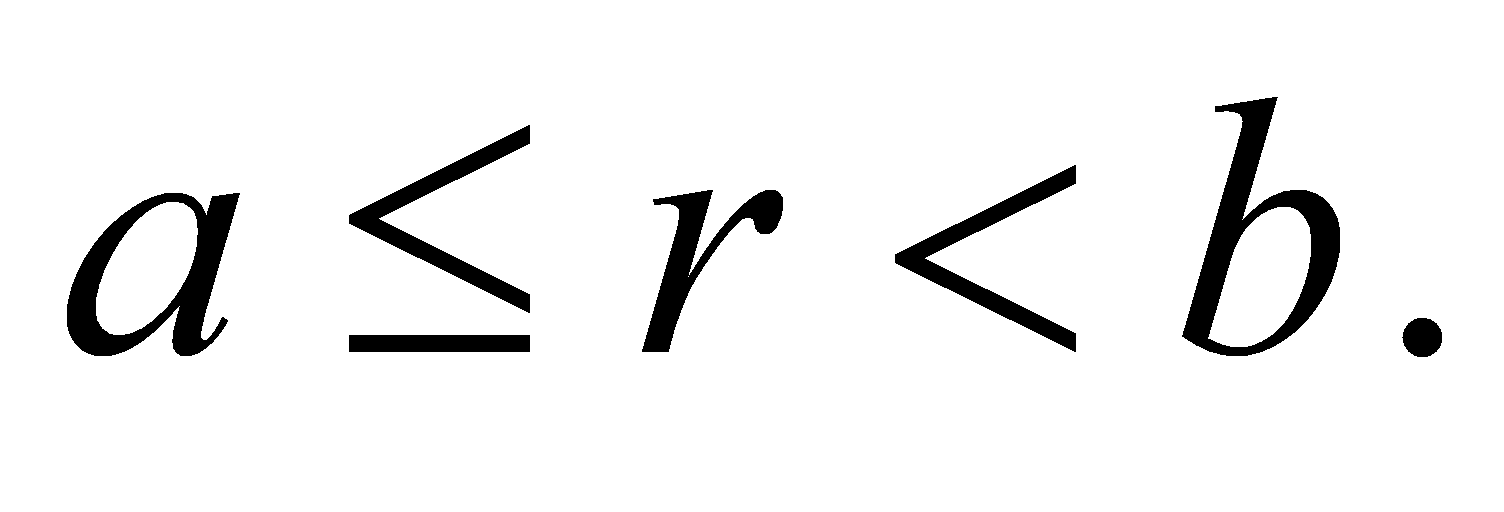
 2018-01-08
2018-01-08 2369
2369
