Принцип разработки алгоритма построения изображений фракталов

1 2 3 4 5 6

Министерство образования и науки Украины

Донбасская государственная машиностроительная академия

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К компьютерному практикуму

по дисциплине

«Современные методы исследования систем»

(для студентов специальности 7.092501 “Автоматизированное

управление технологическими процессами»,

квалификационный уровень – магистр)

Краматорск 2008

УДК 004.438.2

Методические указания к компьютерному практикуму по дисциплине ”Современные методы исследования систем”. (для студентов специальности 7.092501 “Автоматизированное управление технологическими процессами», квалификационный уровень - магистр) / Сост. А. А. Сердюк. – Краматорск: ДГМА, 2008 – 20 с.

Изложены рекомендации по моделированию объектов фрактальной структуры и процессов хаотической динамики.

Составитель А. А. Сердюк, доц.,

Отв. за выпуск С. П. Сус, доц.

МОДЕЛИРОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФРАКТАЛОВ

Цель работы: Освоить методику моделирования фрактальных объектов, описываемых алгебраическими выражениями

Принцип разработки алгоритма построения изображений фракталов

Для построения алгебраических фракталов используются итерации нелинейных отображений, задаваемых простыми алгебраическими формулами.

Наиболее изучен двухмерный случай. Нелинейные динамические системы могут обладать несколькими устойчивыми состояниями. Каждое устойчивое состояние (аттрактор) обладает некоторой областью начальных состояний, при которых система обязательно в него перейдёт. Таким образом, фазовое пространство разбивается на области притяжения аттракторов.

Если фазовым пространство является двухмерным, то, окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.

Алгоритм построения достаточно прост и основан на итеративном выражении:

zi + 1 = F(zi),

где F(z) — какая-либо функция комплексной переменной.

Для всех точек прямоугольной области на комплексной плоскости вычисляем достаточно большое количество раз zi + 1 = F(zi), каждый раз находя абсолютное значение z. При этом значения функции для разных точек комплексной плоскости могут иметь разное поведение:

С течением времени возможны следующие варианты изменения | z |:

• | z | стремится к бесконечности;

• | z | стремится к 0;

• | z | принимает несколько фиксированных значений и не выходит за их пределы;

В общем случае поведение | z | хаотично, без каких-либо тенденций.

Одним из самых распространённых способов раскрашивания точек будет сравнение | z | с заранее выбранным числом, которое считается «бесконечным», т. е. цвет точки равен номеру итерации, на которой |z| достиг «бесконечности», или чёрному в противном случае.

1.2 Примеры построения алгебраических фракталов

Известен алгебраический фрактал KAM Torus, который можно построить с помощью простых алгебраических формул:

x ' = x cos(a) - (y - x ²) sin(a)

y ' = x sin(a) + (y - x ²) cos(a)

Для вычисления этого фрактала используем язык Pascal и создадим программный код в среде Borland Delphi (рис. 1.1)

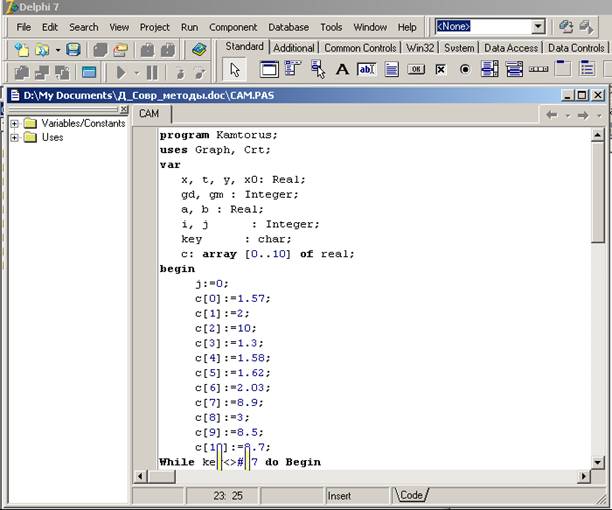
Рисунок 1.1 – Окно редактирования программы в Delphi

Полный текст программного кода приведен ниже.

program Kamtorus;

uses Graph, Crt;

var

x, t, y, x0: Real;

gd, gm: Integer;

a, b: Real;

i, j: Integer;

key: char;

c: array [0..10] of real;

begin

j:=0;

c[0]:=1.57;

c[1]:=2;

c[2]:=10;

c[3]:=1.3;

c[4]:=1.58;

c[5]:=1.62;

c[6]:=2.03;

c[7]:=8.9;

c[8]:=3;

c[9]:=8.5;

c[10]:=8.7;

While key<>#27 do Begin

gd:= Detect;

InitGraph(gd,gm,'c:\bp\bgi');

x:=0;

y:=0;

x0:=0;

repeat

y:=0;

x:=x0;

a:=c[j];

for i:=1 to 10000 do begin

t:=x;

x:=x*cos(c[j])-(y-x*x)*sin(c[j]);

y:=t*sin(c[j])+(y-t*t)*cos(c[j]);

PutPixel(Round(x*150)+320, Round(y*150)+240, 14);

if (x>10)or(y>10) then Break;

end;

x0:=x0+0.01;

until x0>1;

j:=j+1;

if j>10 then j:=0;

key:=Readkey;

end;

CloseGraph;

end.

Изображения фрактала при а = 2, а = 10 приведены на рисунках 1.2, 1.3, соответственно.

Рисунок 1.2 – Изображение фрактала при а = 2

Рисунок 1.3 – Изображение фрактала при а = 10

Алгебраический фрактал «Круги» можно построить с помощью следующего алгоритма: по очереди рассматривается каждый пиксель, затем высчитывается значение z по формуле: z=m*(x²+y²), где x и y - координаты пикселя, а m задает масштаб.

Текст программы, написанный на языке Pascal, приведен ниже:

Program Circle;

Uses Graph, Crt;

Var

x, y, z, l: Integer;

gd, gm: Integer;

mx, my: Integer;

k:real;

Begin

k:=0;

For l:=1 to 10 do

begin