Теплоёмкость в политропном процессе

Так как теплоёмкость зависит от вида процесса, то необходимаформула для теплоёмкости в политропном процессе с_n.

Из общей формулы для теплоёмкостей однородных систем

;

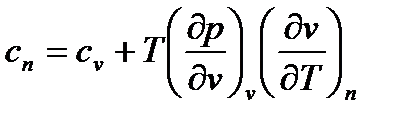пр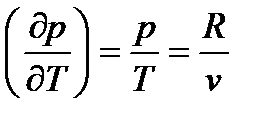и и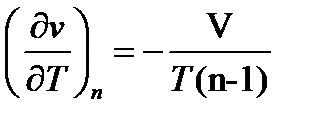

можно получить формулу для массовой (удельной) теплоёмкости в политропном процессе:

Показатель адиабаты k всегда больше единицы, в то время как показатель политропы n может иметь значения от (-¥) до (+¥).

Если n<k, но больше единицы,то значение теплоемкости c_n получаетсяотрицательным.

Отрицательнаятеплоемкость не может быть объясненас физической точки зрения и носит формальный характер, поэтомудальнейшие вычисления работы А,и теплотыQ и внутренней энергииUвыполняются с этим отрицательным значением.

Так как уравнениеполитропы применяется для описания всего множества термодинамических процессов, то изопроцессыможно рассматривать как частные случаи политропного процесса. Такиз уравнения

при n = 0 получается уравнение изобарного процесса(p=const);

при n = 1 – уравнение изотермического процесса(pv=const);

при n = k – уравнение адиабатного процесса (pv^k=const);

При n = ±¥ уравнение политропного процесса превращается в уравнение изохорного процесса(v=const).

n<0

На данном рисунке представлены различные термодинамические процессы с указанием соответствующих значений показателя политропы. Пунктирной линией в качестве примера изображены процессы, не относящиеся к изопроцессам.