2018-01-21
3659
Для любого обратимого процесса dQ = TdS и одновременно dQ = cdT, откуда
dS = c 
.
Тогда для политропного процесса
dSn= 
,
Интегрируя это выражение окончательно получим
формулу для изменения удельной энтропии в политропном процессе:
, Дж/(К*кг).
Подставляя в это уравнение отношениеT2/T1из уравнений Пуассона. получим еще две формулы для расчета измененияя удельной энтропии в политропном процессе:
и 
.
В инженерных расчетах принято полагать, что энтропия равна нулю при нормальных физических условиях. Тогда удельную энтропию можно найти по формулам:
, 
и 
.
19. Исследование изопроцессов идеального газа. Работа, теплота, внутренняя энергия и энтропия в изопроцессах.
19 .1. Изохорный процесс (v = const).
Из общей формулы для абсолютной удельной работы термодеформационной системы 
при dv=0 следует, что работа в изохорном процессе равна нулю:
| Av = 0 |
Изменение удельной внутренней энергии в изохорном процессе при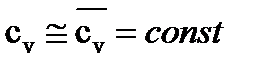 
определяется по формуле:
 |
Из первого начала термодинамики в обычной интегральной форме Q = DU + A, тогда для изохорного процесса Qv = DUv и
удельная теплота в изохорном процессе определяется по формуле:
 |
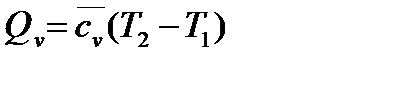Формула для изменения удельной энтропии в изохорном процессе:
19.2. Изотермический процесс (T = const).
Из общей формулы для абсолютной удельной работы термодеформационной системы и уравнения изотермического процеса 
,дающего связь между p и v в виде 
, после подстановки и интегрирования получаем формулы для абсолютной удельной работы термодеформационной системы в изотермическом процессе:
 |
или
 |
или
 |
Внутренняя энергия идеального газа зависит только от температуры, поэтому
изменение внутренней энергии термодеформационной системы в изотермическом процессе равно нулю:
| DUT = 0 |
Из первого начала термодинамики для изотермического процесса:
| QT=AT |
