2018-01-21
740
Каждый из идеальных газов ведет себя в смеси автономно, т. е. так, будто других газов нет. Отсутствие межмолекулярного взаимодействия у идеальных газов обусловливает независимость их свойств от других газов, составляющих смесь. Следствием этой независимости свойств идеальных газов в смеси является строгая аддитивность таких термодинамических величин смеси как давление, внутренняя энергия, энтальпия и т. д.
(Термин «аддитивный» происходит от латинского additivus - полученный путем сложения)
Т. о. вышеперечисленные термодинамические величины для всей смеси получаются путем арифметического сложения соответствующих величин всех компонентов смеси.
Примеры аддитивных величин:масса смеси газов, внутренняя энергия смеси, энтальпия смеси, все термодинамические функции состояния смеси газов, включая характеристические функции (
) и энтропию 
(термодинамический параметр состояния).
Масса смеси:
.
Внутренняя энергия 
смеси nгазов массой 
, занимающих объем 
, равна:
,
где: 
- внутренняя энергия 
килограммов i -го газа в составе
смеси, Дж
Обозначим: uсм - удельная внутренняя энергия смеси газов (внутренняя энергия одного кг смеси), Дж / кг; ui- удельная внутренняя энергия i -го газа смеси, Дж / кг
,
.
Тогда:
Окончательно:
.
Энтальпия смеси 
газов 
, Дж:
,
где: 
- энтальпия 
килограммов i - го газа в составе смеси; 
= 1, 2,.........., 
.
(В формулах для вычисления энтальпии индекс «i» для газа заменен на «
» во избежание совпадения обозначений удельной энтальпии (i) и индекса i -го газа)
По аналогии с внутренней энергией можно получить формулу для удельной энтальпии смеси газов iсм, Дж / кг:
где: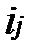 
- удельная энтальпия i -го газа в составе смеси.
Все термодинамические функции состояния смеси газов также обладают свойством аддитивности.К функциям состояния помимо всех характеристических функций () относится также энтропия - термодинамический параметр состояния.
Здесь: 
- свободная энергия (энергия Гельмгольца, изохорно-изотермический потенциал);
- свободная энтальпия (энтальпия Гиббса, изобарный потенциал, изобарно-изотермический потенциал).
Для свободной энергии по аналогии с внутренней энергией и энтальпией смеси можно окончательно записать:
У дельная свободная энергия 
-компонентной смеси газов массой 
, Дж / кг:
,
где: 
- удельная свободная энергия i -го газа смеси, Дж / кг.
Удельная свободная энергия смеси газов, Дж / кг:
,
где: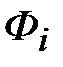 
- удельная свободная энергия i -го газа смеси, Дж / кг
Удельная энтропия смеси газов, Дж / (кг К)
,
где: 
- удельная энтропия i -го газа смеси, Дж / (кг К)
