Математическая формализация задачи

Дана система линейных алгебраических уравнений (СЛАУ) с неизвестными. Требуется решить эту систему: определить, сколько решений она имеет (ни одного, одно или бесконечно много), а если она имеет хотя бы одно решение, то найти любое из них.

Формально задача ставится следующим образом. Решить систему:

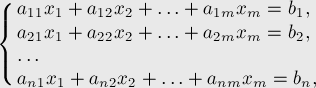
где коэффициенты 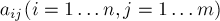и 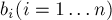известны, а переменные 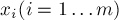— искомые неизвестные.

Удобно матричное представление этой задачи:

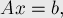
где 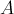— матрица 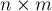, составленная из коэффициентов 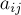, 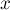и 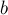— векторы-столбцы высоты .

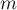Кратко говоря, алгоритм заключается в последовательном исключении переменных из каждого уравнения до тех пор, пока в каждом уравнении не останется только по одной переменной. Если 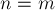,то можно говорить, что алгоритм Гаусса-Жордана стремится привести матрицу системы к единичной матрице — ведь после того как матрица стала единичной, решение системы очевидно — решение единственно и задаётся получившимися коэффициентами .

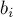При этом алгоритм основывается на двух простых эквивалентных преобразованиях системы: во-первых, можно обменивать два уравнения, а во-вторых, любое уравнение можно заменить линейной комбинацией этой строки (с ненулевым коэффициентом) и других строк (с произвольными коэффициентами).

На первом шаге алгоритм Гаусса-Жордана делит первую строку на коэффициент 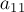. Затем алгоритм прибавляет первую строку к остальным строкам с такими коэффициентами, чтобы их коэффициенты в первом столбце обращались в нули — для этого, очевидно, при прибавлении первой строки к 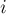-ой надо домножать её на 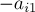. При каждой операции с матрицей 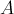(деление на число, прибавление к одной строке другой) соответствующие операции производятся и с вектором 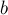; в некотором смысле, он ведёт себя, как если бы он был 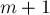-ым столбцом матрицы .

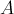В итоге, по окончании первого шага первый столбец матрицы 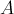станет единичным (т.е. будет содержать единицу в первой строке и нули в остальных).

Аналогично производится второй шаг алгоритма, только теперь рассматривается второй столбец и вторая строка: сначала вторая строка делится на 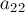, а затем отнимается от всех остальных строк с такими коэффициентами, чтобы обнулять второй столбец матрицы .

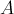И так далее, пока мы не обработаем все строки или все столбцы матрицы 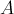.Если 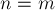, то по построению алгоритма очевидно, что матрица 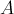получится единичной, что нам и требовалось.

БЛОК-СХЕМА АЛГОРИТМА