Задача №3. Обработка многократных измерений

Задание: Определить вид ЗРВ по критерию Пирсона;

Записать результат с доверительной вероятностью P=0.98

39,15	39,11	38,81	38,92	38,41	38,67	38,91	38,94	38,62	38,91
38,83	39.03	38.65	38.80	38.88	39.37	39.10	39.03	38.99	38.91
39.20	38.98	39.02	38.78	39.02	38.96	38.90	38.78	38.79	39.03
38.89	39.30	38.89	38.85	38.79	38.99	38.86	38.98	38.80	38.77
38.71	39.07	38.76	38.97	38.99	38.59	38.78	39.02	38.42	38.90
38.74	38.73	39.00	38.47	38.52	38.79	39.12	38.83	38.95	39.10
38.68	38.95	38.94	38.67	38.88	38.79	39.13	38.98	38.90	39.22
39.04	38.81	39.01	39.18	38.76	38.67	39.19	38.79	38.85	39.06
39.05	39.16	39.07	39.01	39.09	38.99	38.69	38.73	39.08	38.85
38.79	38.85	38.78	38.84	38.98	38.86	38.88	38.87	39.16	38.97

 

Отсортируем исходные данные по возрастанию

Х
m
Х
m
Х
m
Х
m
Х
m

 

1 Используя полученные данные, найдем значение среднего арифметического Х и оценки среднего квадратического отклонения S_х:

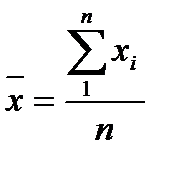
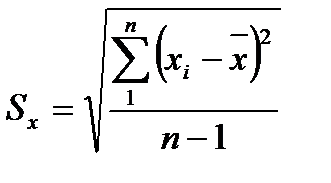
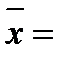
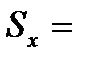
2.С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.

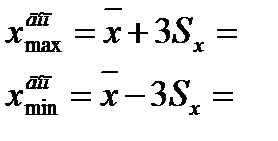
Таким образом, ни один из результатов не выходит за границы интервала [ 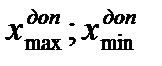], следовательно, с вероятностью 0.9973 гипотеза об отсутствии грубых погрешностей принимается.

3.Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разобьем на k одинаковых интервалов .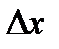

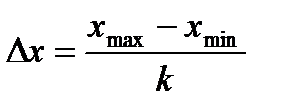
Принимая k=7, получим

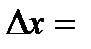
Т.к. в крайние интервалы попадает меньше 5 наблюдений, то объеденим их с соседними.

Результаты производимых вычислений занесем в первую половину таблицы 1, и строим гистограмму.

 

Из вида гистограммы можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.

 

Xi-1

Xi

m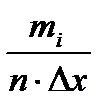

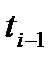
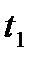
Фi-1

Фi

Pi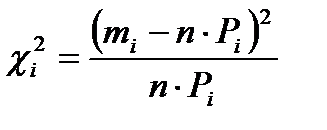

 

 

4.Проверка нормальности закона распределения по критерию Пирсона.

Т.к. в предыдущем пункте выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используем функцию Лапласа:

 

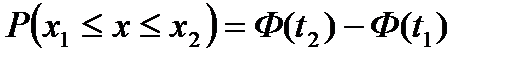
В данном случае значения x₁ и x₂ соответствуют началу и концу интервала. Для каждого из значений нужно рассчитать относительный доверительный интервал 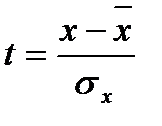, а затем из таблиц функции Лапласа находим соответствующие значения этой функции Ф(t₁) Ф(t₂).

 

Найдя, таким образом, значения P_i для каждого интервала k_i, заполним соответствующие ячейки таблицы, а затем рассчитаем значение c² – критерия для каждого интервала.

 

 

Суммарное значение c²:

 

Определим табличное (критическое) значение c², задавшись доверительной вероятностью 0.97 и вычислив по формуле r=k-3 число степеней свободы:

r=5-3=2

 

 

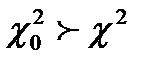
Таким образом, с вероятностью 0.97 гипотеза о нормальности распределения вероятности результата измерения принимается.