Теоретичні основи урівноваження мас, що обертаються

З теоретичної механіки відомо, що тіло, що обертається, не надає динамічних дій на опори у тому випадку, коли головний вектор сил інерції і головний вектор моменту сил інерції ротора дорівнюють нулю. Ця умова завжди виконується, якщо його центр мас лежить на осі обертання і ця вісь є однією з головних центральних осей інерції, тобто ротор цілком урівноважений.

Розглянемо параметри, що характеризують неврівноваже ність ротора, і покажемо, яким чином можна досягти його цілковитої врівноваженості.

Хай ротор I з неврівноваженими масами обертається в опорах 2 з постійною кутовою швидкістю ω₁ (Рис 3.1). Виберемо на роторі точку і з неврівноваженою масою m_і і її координати х_і,;у_і. Радіус-вектор цієї точки r_і; називається ексцентриситетом неврівноваженої маси m_і. Він розташований під кутом α_ί до позитивного напряму осі О_іх_і. Ексцентриситет можна виразити і через його проекції на координатні осі (Рис. 3.1):

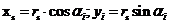3.1

Таких неврівноважених точкових мас в роторі може бути будь-яка кількість.

При обертанні ротора від неврівноваженої точкової маси m_і (Рис.1) виникає сила інерції

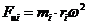3.2

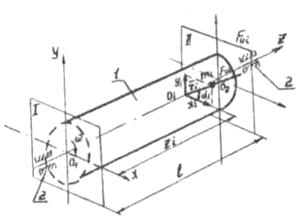
Рис 3.1

 

де добуток m_і г_і - дисбаланс точкової маси m_і обозначаєтся буквою D_і. З урахуванням цього позначення рівність (3.2) набере виду .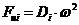

 

Через дві довільно вибрані на роторі точки О₁ і О₂ проведемо площину I і П перпендикулярно до осі обертання ротора. Помістимо в точку О₁ початок координат нерухомої прямокутної системи О₁хуz.

Вісь О₁z направимо уздовж осі обертання ротора, осі О₁х і О₁у розташуємо в площині I.

Перенесемо силу F_ui в площину I паралельно самій собі. Після перенесення отримаємо систему, що складається з сили F_ui, прикладеної в точці О₁, і пари сил з моментом

Мui =F_uiz_i

Таких сил інерції, що сходяться в точці О₁, площини I, і пар сил, що лежать в площинах, перпендикулярних до площини О₁ху і які пересікають вісь О₁z буде стільки, скільки є в роторі неврівноважених мас.

Склавши сили інерції неврівноважених точкових мас і моменти їх пар, знайдемо головний вектор і головний момент від сил інерції по наступних рівнянням, записаним у векторній формі:

 

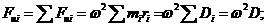	(3.3)
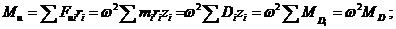	(3.4)

 

де m_i; r_i; D_i; М_Di - відповідно неврівноважена точкова маса, її_эксцентриситет, дисбаланс і момент дисбалансу точкової маси; D_i і М_D - головний вектор і головний момент дисбалансів.

При аналітичному методі визначення головного вектора і головного моменту сил інерції рівняння (3.3) і (3.4) проектуємо на осі х. і у після чого отримуємо

 

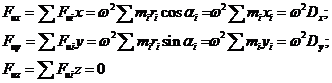(3.5)

 

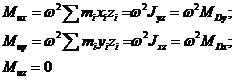(3.6)

де Dх, D|у - проекції головного вектора дисбалансу на осях х і у або статичні моменти точкових неврівноважених мас щодо тих же осей; М_Dу = D_хz; М_Dх = D_уz - проекції головного моменту дисбалансів щодо осей х і у або відцентрові моменти інерції Jуz і Jхz.

З рівнянь (3.5) і (3.6) отримуємо модулі головного вектора сил інерції

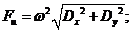(3.7)

і головного їх моменту

 

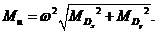(3.8)

Неврівноваженість - це стан ротора, який характеризується таким розподілом мас, який під час обертання викликає змінні навантаження на опорах ротора і його вигин. За міру неврівноваженості вважають дисбаланс D. Для співставлення роторів різних мас вводять поняття «питомий дисбаланс», чисельно рівний ексцентриситету:

 

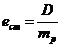де m_р- маса ротора.

Якщо відомі координати центру мас ротора, то його ексцентриситет можна підрахувати по формулі

 

 

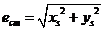3. Види неврівноваженості ротора

Розрізняють статичну, моментну і динамічну неврівноваженість ротора.

Статична неврівноваженість з'являється у випадку, якщо осі обертання ротора I (Рис.4.2,а) і його головна центральна вісь І паралельні. При цьому

 

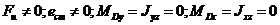Ця неврівноваженість повністю визначається головним вектором дисбалансів D або ексцентриситетом е_ст.

При моментній неврівноваженості вісь ротора 1-1 перетинається в центрі мас S (Рис.3.2, б). При цьому

е_ст = 0; М_Dу=Jух = 0; М_Dу = Jхz = 0, тобто така неврівноваженість повністю визначається головним моментом дисбалансів М_D або його відцентровими моментами інерції. Головний момент дисбалансу підраховується по формулі

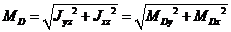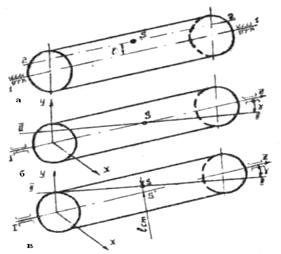
Рис.3.2

 

При динамічній неврівноваженості (Рис.3.2,в), що складається із статичної і моментної, вісь ротора 1-1 і його головна центральна вісь інерції П-П перетинаються не в центрі мас ротора або перехрещуються. В цьому випадку

 

 

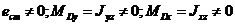тобто динамічна неврівноваженість визначається головним вектором О і головним моментом Ма дисбалансів ротора.

Для усунення додаткового тиску в опорах і коливань станини фундаменту, що викликаються ними, необхідно зрівноважити головний вектор сил інерції Fu і головний момент сил інерції Мu, тобто, щоб вони дорівнювали нулю у будь-який момент руху:

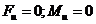Цей процес називається урівноваженням мас, що обертаються, при їх відомому розташуванні або балансуванням ротора при невідомому розташуванні цих мас.