Лабораторне заняття №4

Тема заняття: Симплексний метод розв’язання задач лінійного програмування.

Мета: сформувати вміння та навички розв’язування задач лінійного програмування симплексним методом.

Методичні рекомендації: Вивчити лекцію №3 та ознайомиться з наступною літературою [1 с. 39-52], [2 c. 33-74], [3 с. 32-78].

Постановка завдання:

Процес розв’язування задачі симплекс-методом має ітераційний характер: обчислювальні процедури (ітерації) одного й того самого типу повторюються у певній послідовності доти, доки не буде отримано оптимальний план задачі або з’ясовано, що його не існує.

Отже, симплекс-метод — це поетапна обчислювальна про-
цедура, в основу якої покладено принцип послідовного поліпшення значень цільової функції переходом від одного опорного плану задачі лінійного програмування до іншого.

Алгоритм розв’язування задачі лінійного програмування симплекс-методом складається з п’яти етапів:

1. Визначення початкового опорного плану задачі лінійного програмування.

2. Побудова симплексної таблиці.

3. Перевірка опорного плану на оптимальність за допомогою оцінок Z_j – C_j. Якщо всі оцінки задовольняють умову оптимальності, то визначений опорний план є оптимальним планом задачі. Якщо хоча б одна з оцінок Z_j – C_j не задовольняє умову оптимальності, то переходять до нового опорного плану або встановлюють, що оптимального плану задачі не існує.

4. Перехід до нового опорного плану задачі виконується визначенням розв’язувального елемента та розрахунком нової симплексної таблиці.

5. Повторення дій починаючи з п. 3.

Розглянемо докладніше кожний з етапів алгоритму.

1. Визначення першого опорного плану починають із запису задачі лінійного програмування в канонічній формі, тобто у вигляді обмежень-рівнянь з невід’ємними правими частинами. Якщо в умові задачі присутні обмеження-нерівності, то перетворення їх на рівняння виконується за допомогою додаткових змінних, які вводяться до лівої частини обмежень типу «≤» зі знаком «+», а до обмежень типу «≥» — зі знаком «–». У цільовій функції задачі додаткові змінні мають коефіцієнт нуль.

Після зведення задачі до канонічного вигляду її записують у векторній формі. За означенням опорного плану задачі лінійного програмування його утворюють т одиничних лінійно незалежних векторів, які становлять базис т -вимірного простору (де т — кількість обмежень у задачі лінійного програмування).

На цьому етапі розв’язування задачі можливі такі випадки:

· після запису задачі у векторній формі в системі обмежень є необхідна кількість одиничних векторів. Тоді початковий опорний план визначається безпосередньо без додаткових дій;

· у системі обмежень немає необхідної кількості одиничних незалежних векторів. Тоді для побудови першого опорного плану застосовують метод штучного базису. Ідея його полягає в тому, що відсутні одиничні вектори можна дістати, увівши до відповідних обмежень деякі змінні з коефіцієнтом +1, які називаються штучними. У цільовій функції задачі лінійного програмування штучні змінні мають коефіцієнт + М (для задачі на min) або – М (для задачі на max), де М — досить велике додатне число.

Визначені одиничні лінійно незалежні вектори утворюють базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні — вільними. Їх прирівнюють до нуля та з кожного обмеження задачі визначають значення базисних змінних. У такий спосіб отримують початковий опорний план задачі лінійного програмування.

2. Подальший обчислювальний процес та перевірку опорного плану на оптимальність подають у вигляді симплексної таблиці.

У першому стовпчику таблиці — «Базис» — записують базисні змінні опорного плану, причому в тій послідовності, в якій вони розміщуються в системі обмежень задачі.

Наступний стовпчик симплексної таблиці — «С _баз» — коефіцієнти при базисних змінних у цільовій функції задачі.

У третьому стовпчику — «План» — записують значення базиних змінних і відшукувані у процесі розв’язування задачі компоненти оптимального плану.

У решті стовпчиків симплексної таблиці, кількість яких відповідає кількості змінних задачі, записують відповідні коефіцієнти з кожного обмеження задачі лінійного програмування.

3. Перевіряють опорний план на оптимальність згідно з наведеною далі теоремою.

Теорема (ознака оптимальності опорного плану).
Опорний план задачі лінійного програмування є оптимальним, якщо для всіх 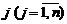виконується умова

(для задачі на max)

або

(для задачі на min)

Якщо для побудови опорного плану було використано метод штучного базису, необхідною умовою оптимальності є також вимога, щоб у процесі розв’язування задачі всі штучні змінні були виведені з базису і дорівнювали нулю.

Значення оцінок визначають за формулою

або безпосередньо із симплексної таблиці як скалярний добуток векторів-стовпчиків «С _баз» та «x_j» мінус відповідний коефіцієнт С_j. Розраховані оцінки записують в окремий рядок симплексної таблиці, який називають оцінковим.

У процесі перевірки умови оптимальності можливі такі випадки:

а) усі задовольняють умову оптимальності, і тоді визначений опорний план є оптимальним;

б) не всі задовольняють умову оптимальності, і тоді потрібно виконати перехід до наступного, нового опорного плану задачі.

4. Перехід від одного опорного плану до іншого виконується зміною базису, тобто виключенням з нього деякої змінної та введенням замість неї нової з числа вільних змінних задачі.

Змінна, яка включається до нового базису, відповідає тій оцінці , що не задовольняє умову оптимальності. Якщо таких оцінок кілька, серед них вибирають найбільшу за абсолютною величиною і відповідну їй змінну вводять до базису. Припустимо, що індекс зазначеної змінної j = k. Відповідний стовпчик симплексної таблиці називають напрямним.

Для визначення змінної, що має бути виключена з базису, знаходять для всіх додатних a_ik напрямного стовпчика величину . Вибирають найменше значення θ, яке вказує на змінну, що виводиться з базису. Припустимо, що це виконується для . Відповідний рядок симплексної таблиці називатиметься напрямним.

Перетином напрямного стовпчика та напрямного рядка визначається число симплексної таблиці a_rk, яке називають розв’язувальним елементом. За допомогою елемента a_rk і методу Жордана—Гаусса розраховують нову симплексну таблицю.

Далі ітераційний процес повторюють доти, доки не буде визначено оптимальний план задачі.

У разі застосування симплекс-методу для розв’язування задач лінійного програмування можливі такі випадки.

1. Якщо в оцінковому рядку останньої симплексної таблиці оцінка Z_j – C_j = 0 відповідає вільній (небазисній) змінній, то це означає, що задача лінійного програмування має альтернативний оптимальний план. Отримати його можна, вибравши розв’язувальний елемент у зазначеному стовпчику таблиці та здійснивши один крок симплекс-методом.

2. Якщо при переході у симплекс-методі від одного опорного плану задачі до іншого в напрямному стовпчику немає додатних елементів a_ik, тобто неможливо вибрати змінну, яка має бути виведена з базису, то це означає, що цільова функція задачі лінійного програмування є необмеженою й оптимальних планів не існує.

3. Якщо для опорного плану задачі лінійного програмування всі оцінки задовольняють умову оптимальності, але при цьому хоча б одна штучна змінна є базисною і має додатне значення, то це означає, що система обмежень задачі несумісна й оптимальних планів такої задачі не існує.

Приклад1.

Продукція чотирьох видів А, В, С і Д проходить послідовну обробку на двох верстатах. Тривалість обробки одиниці продукції кожного виду задано таблицею.

Верстат	Тривалість обробки, год, одиниці продукції
А	В	С	Д

Витрати на виробництво одиниці продукції кожного виду визначають як величини, прямо пропорційні до часу використання верстатів (у машино-годинах). Вартість однієї машино-год становить 10 дол. для верстата 1 і 15 дол. — для верстата 2. Можливий час використання верстатів обмежений: для верстата 1 він становить 450 машино-год, а для верстата 2 — 380 машино-год.

Ціна одиниці продукції кожного виду дорівнює відповідно 73, 70, 55 та 45 дол.

Визначити оптимальний план виробництва продукції всіх чотирьох видів, який максимізує загальний чистий прибуток.

Побудова математичної моделі. Нехай х_j — план виробництва продукції j -го виду, де j може набувати значень від 1 до 4.

Умовами задачі будуть обмеження на час використання верстатів для виробництва продукції всіх видів:

для верстата 1 (машино-год);

для верстата 2 (машино-год).

Цільова функція задачі визначається як загальний чистий прибуток від реалізації готової продукції і складається з різниці між ціною та собівартістю виготовлення продукції кожного виду:

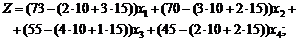
Отже, математична модель поставленої задачі має такий вигляд:

;

Розв’язування. Розв’яжемо задачу симплекс-методом згідно з розглянутим алгоритмом.

1. Запишемо систему обмежень задачі в канонічному вигляді. Для цього перейдемо від обмежень-нерівностей до строгих рівнянь, увівши до лівої частини обмежень додаткові змінні х ₅ та х ₆:

Ці додаткові змінні за економічним змістом означають можливий, але не використаний для виробництва продукції час роботи верстатів 1 та 2. У цільовій функції Z додаткові змінні мають коефіцієнти, які дорівнюють нулю:

Канонічну систему обмежень задачі запишемо у векторній формі:

де

Оскільки вектори та одиничні та лінійно незалежні, саме з них складається початковий базис у зазначеній системі векторів. Змінні задачі х ₅ та х ₆, що відповідають одиничним базисним векторам, називають базисними, а решту — вільними змінними задачі лінійного програмування. Прирівнюючи вільні змінні до нуля, з кожного обмеження задачі дістаємо значення базисних змінних:

Згідно з визначеними векторна форма запису системи обмежень задач матиме вигляд

Оскільки додатні коефіцієнти х ₅ та х ₆ відповідають лінійно незалежним векторам, то за означенням

є опорним планом задачі і для цього початкового плану

2. Складемо симплексну таблицю для першого опорного плану задачі.

Базис	С _баз	План				–5	θ
х ₁	х ₂	х ₃	х ₄	х ₅	х ₆
← х ₅
х ₆
Z_j – C_j ≥ 0		–8	–10

Елементи останнього рядка симплекс-таблиці є оцінками ∆ _j, за допомогою яких опорний план перевіряють на оптимальність. Їх визначають так:

;

У стовпчику «План» оцінкового рядка записують значення цільової функції Z, якого вона набуває для визначеного опорного плану: .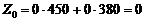

3. Після обчислення всіх оцінок опорний план перевіряють на оптимальність. Для цього продивляються елементи оцінкового рядка. Якщо всі ∆ _j ≥ 0 (для задачі на max) або ∆ _j ≤ 0 (для задачі на min), визначений опорний план є оптимальним. Якщо ж в оцінковому рядку присутня хоча б одна оцінка, що не задовольняє умову оптимальності (від’ємна в задачі на max або додатна в задачі на min), то опорний план є неоптимальним і його можна поліпшити.

У цій задачі в оцінковому рядку дві оцінки та суперечать умові оптимальності, і тому перший визначений опорний план є неоптимальним. За алгоритмом симплекс-методу необхідно від нього перейти до іншого опорного плану задачі.

4. Перехід від одного опорного плану до іншого виконують зміною базису, тобто за рахунок виключення з поточного базису якоїсь змінної та включення замість неї нової з числа вільних змінних.

Для введення до нового базису беремо змінну х ₂, оскільки їй відповідає найбільша за абсолютною величиною оцінка серед тих, які не задовольняють умову оптимальності (│–10│>│–8│).

Щоб визначити змінну, яка підлягає виключенню з поточного базису, для всіх додатних елементів стовпчика «х ₂» знаходимо відношення і вибираємо найменше значення. Згідно з даними симплексної таблиці бачимо, що , і тому з базису виключаємо змінну х ₅, а число а ₁₂ = 3 називатимемо розв’язувальним елементом. Подальший перехід до нового опорного плану задачі полягає в побудові наступної симплексної таблиці, елементи якої розраховують за методом Жордана—Гаусса.

Друга симплексна таблиця має такий вигляд:

Базис	С _баз	План				–5		θ
х ₁	х ₂	х ₃	х ₄	х ₅	х ₆
х ₅			2/3		4/5	2/3	1/3
←х ₆			5/3		–5/3	2/3	–2/3
Z_j – C_j ≥ 0		–4/3		40/3	35/3	10/3

У цій таблиці спочатку заповнюють два перших стовпчики «Базис» і «С _баз», а решту елементів нової таблиці розраховують за розглянутими далі правилами:

1. Розв’язувальний (напрямний) рядок необхідно поділити на розв’язувальний елемент і здобуті числа записати у відповідний рядок нової симплексної таблиці.

2. Розв’язувальний стовпчик у новій таблиці записують як одиничний з одиницею замість розв’язувального елемента.

3. Якщо в напрямному рядку є нульовий елемент, то відповідний стовпчик переписують у нову симплексну таблицю без змін.

4. Якщо в напрямному стовпчику є нульовий елемент, то відповідний рядок переписують у нову таблицю без змін.

Усі інші елементи наступної симплексної таблиці розраховують за правилом прямокутника.

Щоб визначити будь-який елемент нової таблиці за цим правилом, необхідно в попередній симплексній таблиці скласти умовний прямокутник, вершини якого утворюються такими числами:

1 — розв’язувальний елемент;

2 — число, що стоїть на місці елемента нової симплексної таблиці, який ми маємо розрахувати;

3 та 4 — елементи, що розміщуються в двох інших протилежних вершинах умовного прямокутника.

Необхідний елемент нової симплекс-таблиці визначають так:

Наприклад, визначимо елемент 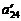, який розміщується в новій таблиці в другому рядку стовпчика «х ₄». Складемо умовний прямокутник:

Тоді . Це значення записуємо в стовпчик «х ₄» другого рядка другої симплексної таблиці.

Аналогічно розраховують усі елементи нової симплексної таблиці, у тому числі елементи стовпчика «План» та оцінкового рядка. Наявність двох способів визначення оцінок опорного плану (за правилом прямокутника та за відповідною формулою) дає змогу контролювати правильність арифметичних обчислень на кожному кроці симплекс-методу.

Після заповнення нового оцінкового рядка перевіряємо виконання умови оптимальності Z_j – C_j ≥ 0 для другого опорного плану. Цей план також неоптимальний, оскільки . Використовуючи процедуру симплекс-методу, визначаємо третій опорний план задачі, який наведено у вигляді таблиці:

Базис	С _баз	План				–5
х ₁	х ₂	х ₃	х ₄	х ₅	х ₆
х ₂						2/5	3/5	–2/5
х ₁					–1	2/5	–2/5	3/5
Z_j – C_j ≥ 0					61/5	14/5	4/5

В оцінковому рядку третьої симплексної таблиці немає від’ємних чисел, тобто всі ∆ _j ≥ 0 і задовольняють умову оптимальності. Це означає, що знайдено оптимальний план задачі:

або

Х ^* = (48; 118; 0; 0; 0; 0);

Отже, план виробництва продукції, що передбачає випуск
48 одиниць продукції А та 118 од. продукції В, оптимальний
і дає найбільший прибуток 1564 дол. При цьому час роботи верстатів використовується повністю (х ₅ = х ₆ = 0).

Задача 1.

Розв’язати задачу лінійного програмування симплексним методом:

1.1. 1.2.