ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЁРДОГО ТЕЛА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: Определение момента инерции однородного прямоугольного параллелепипеда относительно оси симметрии методом крутильных колебаний.
Приборы и принадлежности: Установка лабораторная „Унифилярный подвес“. Электронный блок ФМ 1/1. Набор грузов. Штангенциркуль. Линейка.
Краткая теория
Моментом инерции твердого тела называется физическая величина, характеризующая распределение масс в теле относительно оси вращения и являющаяся мерой инертности тела при вращательном движении.
Твёрдое тело можно представить как совокупность большого числа материальных точек. В таком случае момент инерции твердого тела относительно оси вращения равен сумме моментов инерции всех образующих его материальных точек относительно этой оси и определяется по формуле

где 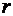 r- расстояние от данной материальной точки массой
r- расстояние от данной материальной точки массой  до оси вращения,
до оси вращения, 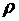 - плотность вещества твердого тела,
- плотность вещества твердого тела,  – объём тела.
– объём тела.
Момент инерции тела зависит от его массы, формы, размеров и положения оси вращения.
 |
Найдём момент инерции однородного прямоугольного параллелепипеда относительно оси симметрии Z (рис. 1).
Совместим начало координат с центром масс параллелепипеда, а координатные оси направим параллельно его граням 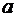 ,
, 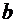 ,
, 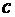 .
.
Для определения момента инерции параллелепипеда относительно оси 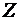 разобьём его на параллельные слои толщиной
разобьём его на параллельные слои толщиной  , высотой
, высотой 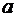 и длиной
и длиной 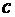 . Каждый слой разобьём на элементарные объёмы в виде столбиков высотой
. Каждый слой разобьём на элементарные объёмы в виде столбиков высотой 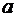 и площадью основания
и площадью основания  (рис.1).
(рис.1).
Масса каждого элементарного объёма  , где
, где 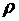 – плотность металла, из которого сделан параллелепипед.
– плотность металла, из которого сделан параллелепипед.
Вклад каждого элементарного объёма в общий момент инерции параллелепипеда  равен
равен
 , (1)
, (1)
где 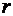 – расстояние столбика до оси вращения (
– расстояние столбика до оси вращения ( ).
).
Момент инерции каждого слоя можно найти, проинтегрировав выражение (1) по  в пределах от
в пределах от  до
до  :
:
 . (2)
. (2)
Для определения момента инерции всего параллелепипеда нужно выражение (2) проинтегрировать по 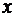 в пределах от
в пределах от  до
до  :
:
 .
.
Откуда следует окончательное выражение:
 . (3)
. (3)
Полученная формула позволяет вычислить значение момента инерции однородного параллелепипеда относительно оси симметрии 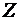 .
.
Однако моменты инерции твёрдых тел относительно заданной оси вращения можно определить и экспериментально.
Для определения момента инерции тела экспериментальным путём в данной лабораторной работе служит установка «Унифилярный подвес» (рис. 2).
Установка состоит из основания 1, вертикальной стойки 2, верхнего 3, нижнего 4 и среднего 5 кронштейнов.
Верхний и нижний кронштейны предназначены для крепления узлов подвески и натяжения стальной проволоки 8, с ней связана металлическая рамка 9, в которой закрепляется исследуемое тело 6.
 |
Если рамку отклонить от положения равновесия и отпустить, она будет совершать колебания. Колебания такого рода называют крутильными. Они происходят под действием упругих сил, возникающих в стальной проволоке 8.
Известно, что период крутильных колебаний относительно оси зависит от момента инерции  колеблющейся системы относительно этой оси:
колеблющейся системы относительно этой оси:
 , (4)
, (4)
где  – постоянная момента упругих сил.
– постоянная момента упругих сил.
Если исследуемое твёрдое тело 6 жёстко закрепить в рамке 9, то для периода колебаний такой системы можно записать:
 , (5)
, (5)
где  - момент инерции рамки, а
- момент инерции рамки, а  - момент инерции исследуемого тела.
- момент инерции исследуемого тела.
Период колебаний рамки без тела определяется соотношением
 . (6)
. (6)
Решая систему уравнений (5) и (6), получим для  выражение
выражение
 . (7)
. (7)
Из формулы (7) следует, что если известен момент инерции рамки, то для нахождения момента инерции исследуемого тела достаточно экспериментально определить периоды колебаний унифилярного подвеса с телом и без него.
Момент инерции рамки также можно определить опытным путём. Для этого на ней нужно укрепить грузы 7 (рис 2). В качестве грузов используются два цилиндра. Период крутильных колебаний рамки с цилиндрами:
 ; (8)
; (8)
где  - момент инерции цилиндра.
- момент инерции цилиндра.
Момент инерции цилиндра можно рассчитать с помощью теоремы Штейнера:
 , (9)
, (9)
где 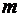 – масса цилиндра,
– масса цилиндра, 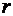 – радиус цилиндра,
– радиус цилиндра,  – расстояние от оси цилиндра до оси вращения.
– расстояние от оси цилиндра до оси вращения.
Из формул (6), (8) и (9) для момента инерции рамки следует выражение, в которое входят экспериментально измеряемые величины:
 . (10)
. (10)
 2018-01-21
2018-01-21 1276
1276








