Частотные характеристики звеназапаздывания

В соответствии с формулой (28) передаточной функ­ции звена W(р) = е^-рτ частотные характеристики запаздывающего звена имеют вид:

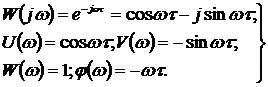(55)

Так как АЧХ такого звена равна единице и не зави­сит от частоты, а ФЧХ пропорциональна частоте с коэф­фициентом пропорциональности, равным τ, то АФХ представляет собой окружность единичного радиуса с цент­ром в начале координат (рис. 25,а).

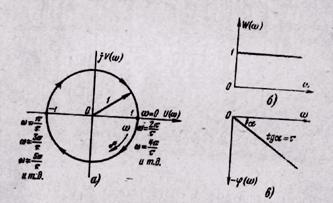
Рис. 25. Частотные характеристики звеназапаздывания.

При ω = 0 вектор АФХ совпадает с положительной вещественной полуосью и конец его расположен в точке (1, j0).

При увеличении частоты конец вектора АФХ повора­чивается по окружности по часовой стрелке, так как ФЧХ отрицательна.

При бесконечном увеличении частоты вектор W(jω) бесчисленное число раз поворачивается вокруг начала координат.

При его повороте на 360° он займет первона­чальное положение. Так как приращение фазы при этом будет равно -2π, то φ(ω) = - ωτ = -2π. Следова­тельно, в исходное положение вектор АФХ вернется при частоте ω = 2π/τ. При дальнейшем увеличении частоты вектор W(jω) будет занимать исходное положение при частотах 4π/τ, 6π/τ, 8π/τ и т. д.

Соответственно отрицательная вещественная полуось будет совпадать с вектором W(jω) при частотах π/τ, 3π/τ, 5π/τ и т. д. и при этом конец вектора будет нахо­диться в точке (-1, j0).

Таким образом, запаздывающее звено на выходе вос­производит входные колебания без искажений по форме, но с отставанием по фазе. Это отставание тем больше, чем больше запаздывание звена и чем больше частота входных колебаний.

Логарифмическая амплитудно-частотная характери­стика звена

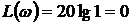(56)

представляет собой прямую, совпадающую с осью абс­цисс. Логарифмическая фазо-частотная характеристика строится по выражению φ(ω) = - τ(ω) в полулогарифми­ческом масштабе.