 +
+ 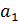 x = 0, u = 0
x = 0, u = 0
Вводим p =  Оператор Лапласа
Оператор Лапласа
x( p +
p + 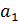 ) = 0,
) = 0,  0 – уравнение в операторной форме
0 – уравнение в операторной форме
ap + 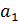 = 0 – характеристическое уравнение
= 0 – характеристическое уравнение
p* = - 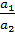 – вектор собственного значения
– вектор собственного значения
x = 
c – собственный вектор с = 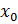

Рис. Устойчивое и неустойчивое апериодическое движение
Для устойчивости линейной системы 1 порядка необходимо, чтобы ее вещественные корень был строго отрицательный. Если система описывается дифференциальным уравнением 1 порядка, то ее движение является апериодичноустойчивым или неустойчивым.
Для устойчивости динамической системы необходимо существование сил или момента, которые будут направлены к положению равновесия при начальном отклонении.
Для асимптотической устойчивости необходимо существование демпфирующего момента, который будет всегда направлен против вектора линейной или угловой скорости.
Пример использования MatLab для определения устойчивости системы 1 порядка.
MatLab 6.5.1
ControlToolbox  линейный анализ и синтез
линейный анализ и синтез
Угловое вращение самолета по крену:
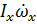 =
= 
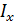 – момент инерции по крену;
– момент инерции по крену;  – коэффициент демпфирующего момента.
– коэффициент демпфирующего момента.
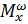 =
= 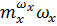
Для расчетов преобразуем в уравнение в форме Кошиотносительно производной
 =
= 
 –элемент динамических коэффициентов
–элемент динамических коэффициентов
Для решения задачи указываем курсором на значок MatLab, загружаем систему и на наборном поле указываем исходные данные:

S = 180
L = 27
V = 200
 = 0.37
= 0.37
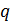 = 0.5 -
= 0.5 -  V
V 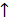 2
2
 = -7.3
= -7.3
 =
=  q
q  S
S  L
L
 =
= 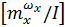
damp (A)
Собственное значение -3.5, коэффициент относительного демпфирования 1, собственная частота 3,5.
 2018-01-21
2018-01-21 785
785








