Частотные характеристики дифференцирующего звена

Частотные характеристики идеального дифференци­рующего звена с передаточной функцией (27) имеют вид:

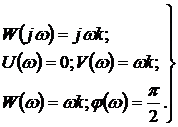(53)

В комплексной показательной форме W(jω) = ωke 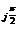. Эти характеристики представлены на рис. 23.

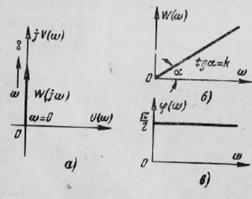
Рис. 23. Частотные характеристики дифференцирующего звена.

Амплитудно-фазовая характеристика дифференциру­ющего звена совпадает с положительной мнимой полу­осью (рис. 23,а).

При всех частотах выходные колебания опережают по фазе входные колебания на угол 90°, так как фазо-частотная характеристика φ(ω) не зависит от ча­стоты и равна π/2 (рис. 23,в).

Амплитудно-частотная характеристика W(ω) имеет вид прямой линии, проходящей через начало координат под углом α = arctgk. Чем больше частота входных колебаний, тем больше они усиливаются звеном. При малых частотах (ω ≈ 0) сигнал через звено не проходит (рис. 23,б).

Скачкообразное единичное изменение входной вели­чины вызывает мгновенное изменение выходной величи­ны от 0 до ∞ и мгновенный спад ее от ∞ до 0.

Логарифмируя W(ω) в выражении (53), получаем:

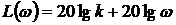. (54)

Логарифмическая амплитудно-частотная характери­стика дифференцирующего звена представляет собой прямую (рис. 24,а) с наклоном +20 дб/дек, ордината которой при ω = 1 равна 20 lgk.

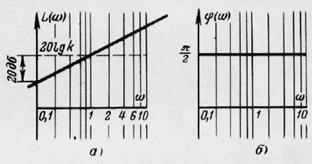
Рис. 24. Логарифмические частотные характеристики дифференцирующего звена.

Фазово-частотная характеристика звена в полулогариф­мическом масштабе в соответствии с (53) представ­лена на рис. 24,б.