Анализ и синтез динамической системы в пространстве состояний

Рассмотрим дифференциальные уравнения движения в линейной стационарной системе:

= + n m

И алгебраические уравнения измерителя:

= +

Эти уравнения записаны в матричной форме. Для исследования системы необходимо ввести элементы матрицы

В векторной форме:

= Ax + Bu

y = Cx + Du

Здесь А – матрица динамических коэффициентов;

В – матрица управления;

C иD – матрицы измерений

Исследование устойчивости представляет собой анализ собственного возмущенного движения в случае равенства нулю управления и начальным отклонении координат: u = 0, x (t=0) =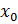

Понятие Ляпунова об устойчивости:

Если линейная система выведена из положения равновесия и затем совершает движение в Ɛ-окрестности положения равновесности (x = 0), то динамическая система устойчива.

Ɛ

Динамическую систему называют асимптотически устойчивой, если предел ее движения заканчивается в положении равновесия.

0 = 0