Аперіодична ланка ІІ порядку

• Передавальна функція: 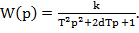• 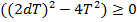, 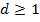.   Перехідна характеристика:
h k t	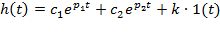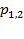- корені характеристичного рівняння

Частотні функції:

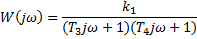
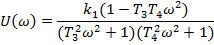
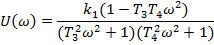
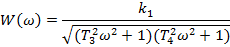
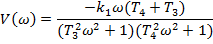
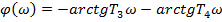
Логарифмічна амплітудна частотна характеристика ланки має вигляд:

-

 

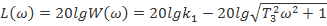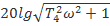
Асимптотична характеристика будується для трьох діапазонів:

 

1) при		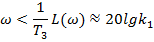-горизонтальна пряма;
2)при		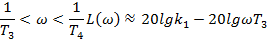-прямаз нахилом -20дБ/дек;
3) при		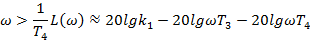- пряма з нахилом -40дБ/дек.

L

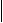20 lgk₁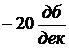

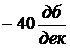
1/ T₃ 1/ T₄ lgω

 

Аперіодична ланка другого порядку може бути представлена як послідовне з’єднання двох аперіодичних ланок першого порядку, що не можна зробити для чисто коливальної ланки:

=

,

 

 

 

,

 

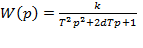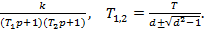
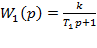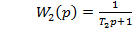
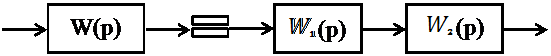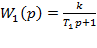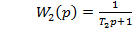
Аперіодична ланка другого порядку – не є елементарною ланкою.

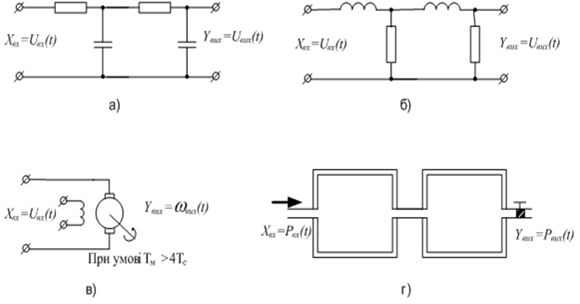
Приклади аперіодичних ланок другого порядку:

а – подвійний RC ланцюжок; b – подвійний LR ланцюжок;

c – електричний двигун; d – два резервуари стиснутого повітря

 

 

Коливальна ланка

Коливальні ланки -це ланки, в яких виникають коливальні процеси.

• Передавальна функція: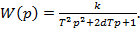

 

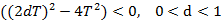• .. Корені характеристичного рівняння комплексно – сполучені: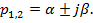

 

• Перехідна функція: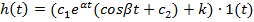

 

 

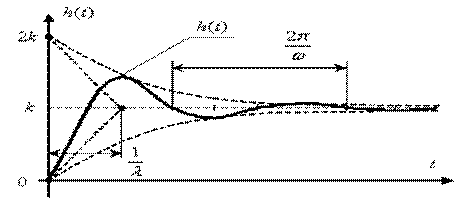
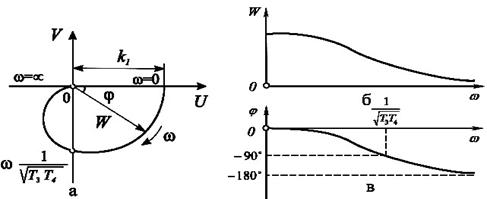
• Частотні функції (: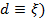

 

,

 

 

 

 

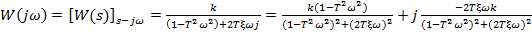
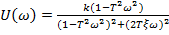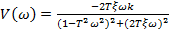
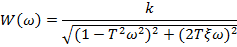
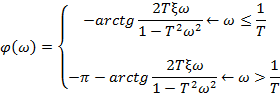
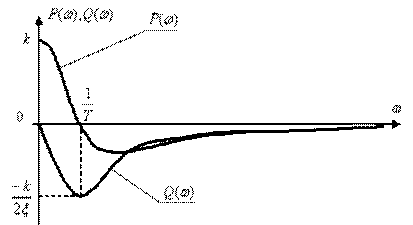
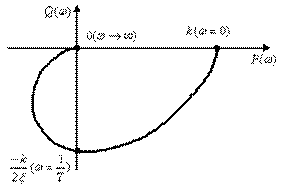
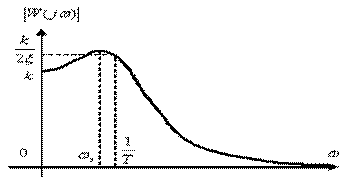
Амплітудна характеристика зменшується зі збільшенням ω, тобто

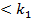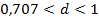W(ω) якщо . При 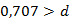з'являється «резонансний пік» на характеристиці W(ω), що іде в нескінченність при 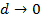. Тому величина 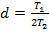називається параметром загасання, збільшення якого веде до зменшення коливань і зменшенню резонансного піку характеристики W(ω). Звідси ясна роль сталих часу 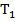і 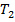у рівнянні ланки: стала 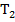«розхитує» коливання, а 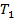- «демпфірує» їх.

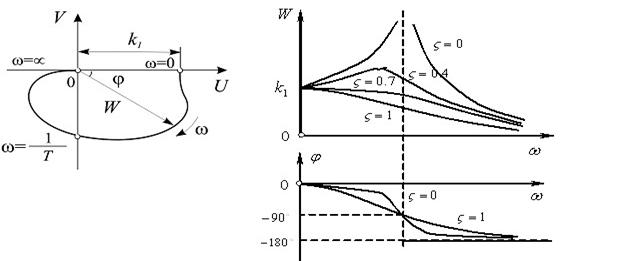
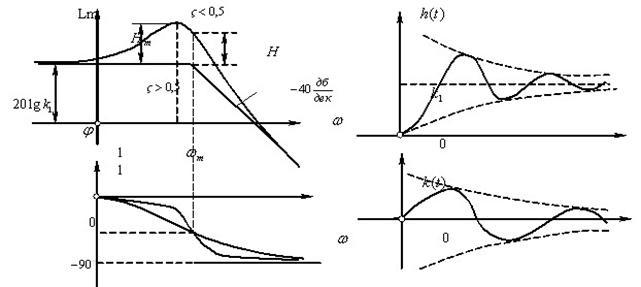
Логарифмічна амплітудна частотна характеристика ланки:

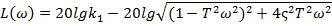
Перший доданок характеристики являє собою горизонтальну пряму, а другий доданок має різний вигляд для різних значень ξ (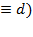:при d=1 ЛАХ співпадає з ЛАХ аперіодичної ланки 2-го порядку; при значеннях 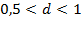характеристика близька до ламаної; при 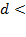0,5 помітний резонансний пік, висота якого дорівнює:

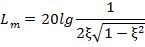
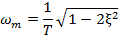
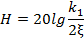
У спрощених розрахунках досить знайти при ω=1/T.

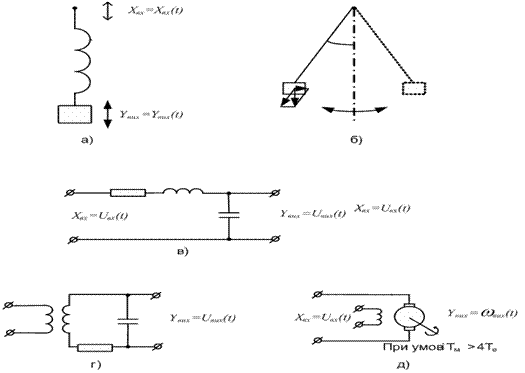
Приклади коливальних ланок: a) вантаж на пружній підвісці, б) маятник, в) LC ланцюжок, г) коливальний контур д) електричний двигун.