Рівняння ланки другого порядку

Диференціальне рівняння ланки другого порядку:

+ +

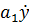Тут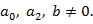

В стандартній формі рівняння має вигляд:

+

Тут , , , - коефіцієнт підсилення, d - коефіцієнт демпфірування, який визначає схильність ланки до коливань.

Передавальна функція ланки другого порядку:

Характеристичне рівняння:

Корені цього рівняння: .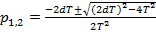

В залежності від коефіцієнта демпфірування корені можуть бути дійсними (речовими) або комплексно - сполученими, що призводить до різних перехідних процесів в ланці.

1) Якщо 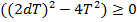,, то корені – дійсні. Це можливо, якщо (аперіодичні ланки 2-го порядку).

2) Якщо то корені комплексно – сполучені. При цьому якщо ланки – коливальні. Якщо , ланка – консервативна.

3) Якщо ланка – немінімально-фазова.