2018-01-21
857
Как было показано ранее (§2.3.) напряжение и ток в любой точке сечения линии с РП выражается уравнениями:
В данных уравнениях комплексные постоянные могут быть определены несколькими способами, если известны граничные условия (либоỦ1 и Ỉ1 в начале, либо Ủ2 и Ỉ2 в конце линии при конкретном режиме работы линии. Рассмотрим 2 наиболее важных, чаще всего встречающихся на практике случаях.
1 случай Ủ1 и Ỉ1 в начале линии (х=0)
Получим из уравнений
Подставим значения 
в исходное уравнение
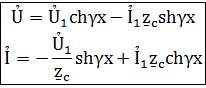
Эти формулы позволяют определить ток и напряжение в любой точке линии о их значениямỦ1 и Ỉ1 в начале линии. Следует отметить чтоchγх иshγх являются комплексными числами, т.к. γх=αх+jβx.
2 случай Ủ2 и Ỉ2 в конце линии (х=0)
При этом можно полагать, что задано сопротивление нагрузки, т.к.
В этом случае удобнее отсчет расстояния вести от конца линии. Примем расстояние до точки от конца линии x’=l-x(где l- длина линии).
При этом имеем
Подставим эти выражения в исходную систему уравнений
После постановки получаем
Введем обозначения 
и получим
При х’=0 т.е. x=l имеем Ủ=Ủ2, Ỉ=Ỉ2
Поэтому 
Решаем совместно находим 
и 
и подставляем их в исходную систему.
Эти формулы позволяют определить ток и напряжение в любой точке линии по их значениям Ủ2 и Ỉ2 в конце линии
