Как вводить аксиомы, если подходить к ним неформально?

Одна из целей включения аксиом в школьный учебник - сформи­ровать базу для построения системы определений и доказательств. По­явление первых доказательств без формулирования необходимых для этого аксиом сродни своего рода фокусам - объявляется, что что-то до­казано, но как доказано и доказательство ли это вообще остается непо­нятным. Непонимание учебного материала часто вызывается именно нечетким его изложением. Окажутся ли аксиомы средством нежелатель­ного формализма, или не окажутся, зависит оттого, как ими воспользо­ваться, какие цели поставить перед их введением и использованием в обучении. Аксиоматический метод заслуживает уважения в школьном обучении еще и потому, что он является главенствующим методом в изложении (построении) математической науки.

Необходимо иметь в виду, что в качестве аксиом обычно выбира­ются уже известные из пропедевтического курса факты или факты, близ­кие к наглядным представлениям учащихся, их жизненному опыту. При этом новым для учащихся является, главным образом, не содержание аксиом, а предельно точный математический язык, на котором они формулируются. Использование аксиом в качестве основы для форми­рования математического языка школьников - одна из основных дидак­тических целей введения и использования аксиом. На основе аксиом в начале курса происходит активное усвоение учащимися математичес­кой терминологии, необходимой для изучения всего курса. Школьник, плохо владеющий математическим языком, окажется неспособным вос­принимать ни текст учебника, ни речь учителя. К первым аксиомам, определениям, теоремам и доказательствам необходимо подходить не как к обычному наращиванию знаний, а как средству развития мате­матической речи.

В психологическом плане важно само начало, то как предстают аксиомы перед школьниками. Одно дело, как нечто совершенно новое, в отрыве от предыдущих знаний, либо как средство систематизации и повторения ранее известных знаний, что в начале систематического школьного курса геометрии является естественным. Если подойти к аксиомам именно с такой позиции, то о каком формализме можно гово­рить? Введение аксиом в контексте известных пропедевтических зна­ний по геометрии делает их намного доступнее любого последующего фактологического материала.

Дидактические формы приведения аксиом в учебнике могут быть различными. Не следует стремиться к формальному стилю их изложе­ния.

Мы неоднократно обращались к пособию геометрии А.В. Погорелова по той причине, что это первое отечественное учебное пособие, в котором приводится полный список аксиом. В нем приводятся аксио­мы принадлежности, порядка, измерения отрезков и углов, откладыва­ния отрезков и углов, существования треугольника, равного данному, параллельности, измерения площадей. Наличие аксиом измерения мак­симально упростило чрезвычайно трудный в математическом отноше­нии вопрос о введении меры для отрезков и углов. Аксиомы откладыва­ния отрезков и углов позволили строго доказать признаки равенства треугольников, что редко встречается в школьном учебнике. В пос­леднем издании этого пособия имеют место определенные ограниче­ния сферы применения этих аксиом. Удачно подобранная система ак­сиом во многом обеспечила рациональное и простое построение всего курса.

2.2.Методические приемы ознакомления учащихся с основны­ми свойствами.

Прежде всего, выясним вопрос: «на использование какой мето­дики ознакомления учащихся с аксиомами ориентируют существующие пособия?» В некоторых пособиях применен своеобразный методичес­кий подход (насколько нам известно, он предложен польским методиком-математиком, автором школьных учебников 3.Крыговской).Вна­чале слова «аксиома», «теорема», «доказательство» даже не употребля­ется, вместо них говорят: «основное свойство», «свойство», «объясне­ние».Вместо выражений «скажите определение» или «сформулируйте определение» используются выражения «какая фигура называется...» или «что такое...».

Термины «аксиома», «теорема», «доказательство» вводятся и разъяс­няются в конце первого параграфа, или даже в конце первой главы - лишь после того, как учащиеся приобретут некоторый опыт примене­ния аксиом в доказательствах. В результате осуществляется неформаль­ное и ненавязчивое введение аксиом, а разъяснение их роли становится более конкретным и убедительным.

Указанный подход к аксиомам применяется в целом ряде современ­ных школьных учебников (3.Крыговская, А.В. Погорелое, Н.М. Рога-новский, И.Ф. Шарыгин и др.)

Остановимся на методике изучения основных свойств. При введе­нии основных свойств можно воспользоваться следующей методичес­кой схемой:

1) мотивация введения основных свойств

2) обращение к наглядной основе;

3) формулирование основного свойства;

4) логический анализ формулировки основного свойства;

5) формирование навыков математической речи;

6) закрепление с помощью математического диктанта;

7) выяснение того, какими свойствами вводимое понятие обладать не может.

I. Основные свойства принадлежности.

Мотивация. Обращение к наглядной основе. Что такое «точка» и «прямая»? Эти понятия вам хорошо знакомы. Представ­ление о точке дают маленький кружочек, пятнышко, след на бумаге от ножки циркуля; о прямой - луч света, туго натянутая нить или шнур (рис. 1, а - в).

Для построения прямых пользуются специальным чертежным ин­струментом-линейкой (рис. 1, г).

 

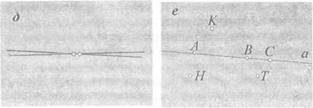
Рис. 1

Формулирование основных свойств:

1 (основные свойства прямой). Для каждой прямой существует сколько угодно точек, принадлежащих этой прямой, и сколько угодно точек, не принадлежащих ей.

Через любые две различные точки можно провести прямую и толь­ко одну.

Логический анализ формулировки основного свойства. Кроме наглядного введения основных свойств, нужно проводить еще краткий логический анализ их формулировки, необхо­димый для выяснения точного математического смысла, анализ ее ло­гического строения. Логический анализ помогает учащимся быстрее привыкнуть к точной математической форме выражения фактов, разви­вает их математическую речь, облегчает им восприятие математичес­кой информации.

Формирование навыков математической речи. Формулировка ос­новного свойства закрепляется путем воспроизведения ее учащимися. В плане развития речи полезно сразу предупредить учащихся, что не­правильно говорить «прямая соединяет две точки». Две точки можно соединить отрезком, а про прямую надо говорить так, как указано в основном свойстве - «прямая проходит через две точки».

Составной частью математической речи (письменной) является оз­накомление учащихся с математической символикой. Говорим, что на рисунке 3 изображена прямая а и точки А, В и С, принадлежащие этой прямой. Нарисованы также точки К, Н и Т, не принадлежащие прямой а.

Закрепление с помощью математического диктанта.

Закрепление практических навыков построения прямых и то­чек и усвоение соответствующей математической терминологии могут быть осуществлены с помощью математического диктанта.

Постройте прямую а.

Отметьте точки А и В, принадлежащие прямой а.

Постройте точки С и Д не принадлежащие прямой а.

Постройте две пересекающиеся прямые с и d (I. Обозначьте бук­вой A точку пересечения этих прямых. Постройте точку В, принадлежа­щую прямой с, но не принадлежащую прямой d. Отметьте точку С, при­надлежащую прямой d, но не принадлежащую прямой с.

II. Основные свойства расположения. Рассмотрим следующие ак­сиомы.

1) Из трех точек на прямой одна, и только одна, лежит между двумя другими.

2) Прямая разбивает плоскость на две полуплоскости. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекается с прямой. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекается с прямой.

Необходимо обратить внимание на возможности мето­дики. Эти возможности практически неограниченные. К примеру, что может быть интересного в таком тривиальном утверждении, как «из трех точек на прямой одна, и только одна, лежит между двумя други­ми»? На первый взгляд, кажется, что вгаком утверждении ничего инте­ресного для ученика не содержится и содержаться не может. Так оно и будет, если ограничиться формальным введением. Совсем другое дело, если учитель сразу приведет задачу, которая покажется ученикам нео­жиданной и, больше того, интересной.

III. Основные свойства измерения отрезков и углов. Они выража­ются следующими предложениями:

1. Каждый отрезок имеет определенную длину, большую нуля. Дли­на отрезка равна сумме длин частей, на которые он разбивается любой своей точкой.

2. Каждый угол имеет опре­деленную градусную меру, боль­шую нуля. Развернутый угол ра­вен 180°. Градусная мера угла равна сумме градусных мер уг­лов, на которые он разбивается любым лучом, проходящим между его сторонами.

Основные свойства измере­ния углов обычно вводятся с опорой на практику измерения углов с помощью транспортира. Угол определяется как фигура, образованная двумя лучами, выходящими из одной точки. Градусная мера такого угла не может быть больше 180°. Вводится также понятие об измерении дуг окружности и Центрального угла окружности. Центральный угол окружности может иметь меру, большую 180°. Объясняется этот факт тем, что централь­ный угол окружности — существенно новое понятие по сравнениюс понятием угла. Центральный угол окружности - это фигура, образо­ванная углом и дугой, заключенной между его сторонами. Мера этой дуги определяет меру центрального угла окружности. Введенные поня­тия обеспечивают все потребности школьного курса геометрии, свя­занные с измерением различных углов.

IV. Основные свойства откладывания отрезков и углов, а также основное свойство равных треугольников характеризуются следующи­ми предложениями.

1) На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

2) От любой полупрямой в заданную полуплоскость можно отло­жить угол с заданной градусной мерой, и только один.

3) Если две стороны и угол между ними одного треугольника соот­ветственно равны двум сторонам и углу между ними другого треуголь­ника, то такие треугольники равны.

Последнее основное свойство является первым признаком равен­ства треугольников. В логическом плане принятие первого признака равенства треугольников является законным - получаем одну из экви­валентных аксиоматик существующим (например, аксиоматике, приня­той в школьном учебнике геометрии А.В. Погорелова). В дидактичес­ком плане принятие такой аксиомы крайне выгодно. Сокращается це­почка доказательств (не нужно доказывать первый признак), получаем аксиому с очень широкой областью применений (в отличие от аксиом, которые имеют буквально одно-двухразовые применения).

V. Основное свойство параллельных прямых: Через точку, не лежа­щую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Иногда в VII классе вводят заключительные основные свойства - основные свойства площади.

В целях выработки навыков правильного употребления математи­ческой терминологии полезны математические диктанты. Желательно, чтобы математический диктант (особенно при крупноблочном изложе­нии учебного материала) охватывал термины по достаточно большому блоку учебного материала. В этом случае диктант положительно ска­зывается на формировании у учащихся системы знаний.

Приведем пример «сквозного» математического диктанта:

«Фигура, образованная... называется углом.

Если стороны ОА и ОВ угла AОВ..., то угол АОВ называется развер­нутым.

Два угла называются равными, если....

Угол называется прямым...; тупым...; острым...

Если две прямые..., то они называются перпендикулярными.

Луч, проходящий..., называется биссектрисой угла.

Два угла называются смежными,....

Два угла называются вертикальными,...».

Роль основных свойств в формировании представлений учащихся об исходных геометрических понятиях. Не нужно упускать возможность выяснения роли основных свойств в формировании представлений об исходных понятиях геометрии. Полезно иметь в виду, что каждая акси­ома - это не только некоторое «отправное» предложение для доказа­тельства теорем, или средство развития математической речи, оно яв­ляется также средством, помогающим уточнить представление о гео­метрических фигурах. Выше акцент был сделан на том, какими свой­ствами обладает прямая. Интересно задаться вопросом: «А какими свой­ствами она обладать не может?» (см. п. 7 методической схемы). Напри­мер, аксиома «Через любые две различные точки можно провести пря­мую и только одну» определяет «прямолинейную» форму прямой. Пря­мая в силу этого основного свойства не может иметь криволинейную форму, так как в этом случае через две точки можно провести не одну кривую, а сколько угодно кривых (рис. 2, а).

Рис. 2

Аксиома «Из трех точек, принадлежащих некоторой прямой, суще­ствует точка, которая лежит между двумя другими» позволяет проде­монстрировать дополнительную особенность прямой - прямая не явля­ется замкнутой линией. Если допустить, что прямая может быть замк­нутой линией (рис. 2, б), то одновременно можно посчитать, что точ­ка С лежит между точками А и В, точка В лежит между точками С и А, точка А лежит между точками В и С. Это противоречит единственности точки, лежащей между двумя другими (для трех точек, принадлежа­щих одной прямой).

Основное свойство «Прямая разбивает все точки плоскости, не при­надлежащие этой прямой, на две полуплоскости» означает, что прямая является неограниченной фигурой. Если бы, например, прямая была ограниченной линией (рис. 2, в), то точки А и В. принадлежащие «до­полнительным» полуплоскостям, оказались бы соединенными отрез­ком АВ, не пересекающим данную «прямую». В этом случае о полу­плоскостях говорить было бы нельзя (была бы только одна «плоскость»).

Полезно привести историческую справку о том, как Пифагор и его ученики отстаивали свою точку зрения о том, что точка не имеет разме­ров, а прямая не имеет толщины. Не сразу эта точка зрения была вос­принята в математике. Интересным окажется также описание, приве­денное в «Началах» Евклида: точка - это то, что не имеет частей, линия есть длина без ширины и т.п.

Необходимо также учитывать, что на формировании геометричес­ких представлений ощутимо сказывается практика выполнения пост­роений фигур. Выполнение построений тонкими линиями больше со­ответствует правильным геометрическим представлениям, приучает учащихся к точности в построениях. Учитывая это, мы не советуем изоб­ражать, например, точки крупными черными кругами, напоминающи­ми «чугунные» шары.

Выше говорилось об опыте учебника геометрии А.П.Киселева, подсказывающем одну из удачных в методическом отношении форм приведения аксиом. Такая форма актуальна и в настоящее время. Она принята, например, в книге Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадом­цева, Э.Г. Позняка «Геометрия: Пробный учебник для шестого класса» (М.: Просвещение, 1987. - 127 с.). Аксиомы в этом учебнике формули­руются, но без внешнего подчеркивания формально-логического аспекта (они не нумеруются, не сообщаются названия групп и т.д.). Формаль­но-логический аспект не подчеркивается и в первых доказательствах данного курса. Непосредственные ссылки на аксиомы в этих доказа­тельствах не делаются (они подразумеваются и при необходимости в устном изложении на уроке могут быть сделаны). Такому приему свой­ственны неформальный стиль изложения и активное обращение к на­глядности в первых доказательствах. Ссылки в доказательствах появ­ляются после изучения признаков равенства треугольников. Подобная «маскировка» аксиом позволяет выдвинуть на первый план наглядно­-геометрическую (содержательную) сторону доказательств. Доказатель­ства при этом оказываются более тесно связанными с возможными ин­туитивными рассуждениями учащихся. Это, безусловно, помогает учащимся в усвоении начала курса. Отмстим одно принципиальное отли­чие данного учебника от учебника А.П.Киселева: возможность форма­лизации начала курса (четкое выделение аксиом, ссылок в первых до­казательствах). При необходимости это можно сделать вместе с учащи­мися (например, в целях осуществления дифференцированного обуче­ния или при повторении курса, при подготовке экзаменов). Прием из­ложения, который дает возможность сравнительно легко «восстановить» дедуктивный стиль, на наш взгляд, является ценным. В приложении к учебнику Л.С. Атанасяна и др. приводится 17 аксиом, которые включа­ют в себя три аксиомы принадлежности, три аксиомы порядка, восемь аксиом наложения и равенства фигур, две аксиомы измерения отрез­ков. Систему аксиом планиметрии завершает аксиома параллельных прямых.

2.3.О введении первых понятий. Учителю необходимо иметь в виду, что ряд математических понятий являются неопределяемыми (в школьном курсе список неопределяемых понятий обычно избыточный). Такими понятиями обычно являются: «точка», «прямая», «точка при­надлежит прямой», «точка В лежит между точками А и С», «полуплос­кость», «длина отрезка», «мера угла», «отложить отрезок (угол) задан­ной меры». Свойства неопределяемых понятий описываются основны­ми свойствами. Все остальные понятия — определяемые. Примерами таких понятий являются: «отрезок», «полупрямая», «угол», «разверну­тый угол», «луч проходит между сторонами угла», «треугольник», «угол треугольника», «равные треугольники», «параллельные прямые» и др.

Одним из центральных понятий для всего курса геометрии являет­ся понятие равных треугольников. В учебнике А.П. Киселева равенство треугольников определяется с помощью наложения (причем это поня­тие математически никак не описывается, целиком и полностью опира­ются на наглядные представления). В пособии под редакцией А.Н. Кол­могорова сразу вводится с помощью перемещения общее понятие ра­венства фигур. Можно утверждать, что определение равенства треуголь­ников через равенство соответственных сторон и углов, приводимое в пособии А.В. Погорелова и в ряде последующих пособий, для школь­ной практики является новым.