Найбільш повна характеристика випадкової величини дається її функцією розподілу (або також і щільністю розподілу для неперервної випадкової величини). Проте досить часто доцільно обмежитися простішою, хоч і неповною інформацією про випадкову величину. Наприклад, досить вказати окремі числові величини, які певним чином визначають істотні риси розподілу випадкової величини: деяке середнє значення випадкової величини; деяке число, що характеризує ступінь розсіювання значень випадкової величини навколо її середнього значення, тощо. Користуючись такими характеристиками, ми в стислій формі можемо отримати інформацію про істотні особливості законів розподілу випадкової величини.
Характеристики, що виражають в стислій формі найістотніші особливості закону розподілу випадкової величини, називаються числовими характеристиками випадкової величини.
До них в першу чергу відносяться математичне сподівання і дисперсія.
5.1. Математичне сподівання.
Випадкова величина може приймати різні числові значення, тому практично важливим є середнє значення випадкової величини. Для оцінки середнього (у ймовірнісному сенсі) значення випадкової величини вводиться поняття математичного сподівання, яке є дійсним середнім значенням випадкової величини і визначається з врахуванням різних ймовірностей її окремих значень.
Математичне сподівання випадкової величини 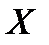 позначаємо
позначаємо 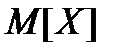 . Для дискретної випадкової величини
. Для дискретної випадкової величини 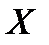 , заданої рядом розподілу
, заданої рядом розподілу
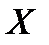
| 
| 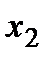
| … | 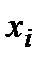
| … | 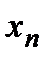
| … |

| 
| 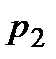
| … | 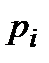
| … | 
| … |
де 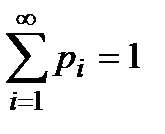 , математичне сподівання обчислюється за формулою
, математичне сподівання обчислюється за формулою
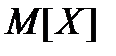 =
= 
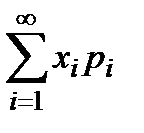 , (1)
, (1)
якщо ряд справа збігається.
Нехай 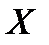 - неперервна випадкова величина, значення якої
- неперервна випадкова величина, значення якої  , і
, і  - її щільність розподілу. Розіб’ємо відрізок
- її щільність розподілу. Розіб’ємо відрізок 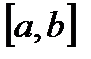 на
на 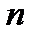 частин, довжини яких
частин, довжини яких 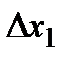 ,
, 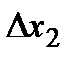 ,…,
,…,  . Візьмемо в кожному частинному відрізку
. Візьмемо в кожному частинному відрізку 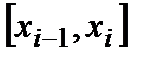 точку
точку 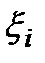 . Добуток
. Добуток 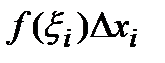 приблизно дорівнює ймовірності попадання неперервної випадкової величини в інтервал
приблизно дорівнює ймовірності попадання неперервної випадкової величини в інтервал  , а сума
, а сума  наближено дорівнює математичному сподіванню неперервної випадкової величини. Якщо існує границя
наближено дорівнює математичному сподіванню неперервної випадкової величини. Якщо існує границя 
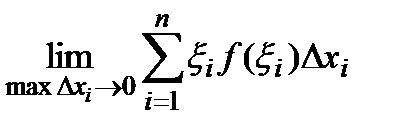 , то вона називається математичним сподіванням неперервної випадкової величини і позначається
, то вона називається математичним сподіванням неперервної випадкової величини і позначається 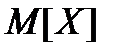 =
= 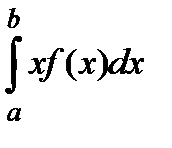 . (2)
. (2)
У випадку, якщо  , то
, то 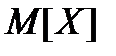 =
=  , причому інтеграл повинен збігатися абсолютно. Відзначимо найпростіші властивості математичного сподівання:
, причому інтеграл повинен збігатися абсолютно. Відзначимо найпростіші властивості математичного сподівання:
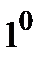 .
.  ; де
; де  - стала величина,
- стала величина,
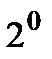 .
. 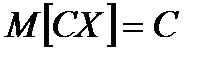
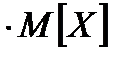 ;
;
 .
. 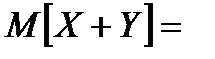
 +
+ 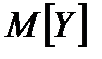 ;
;
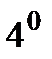 .
. 

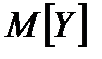 ; якщо випадкові величини
; якщо випадкові величини 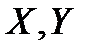 незалежні.
незалежні.
Дві випадкові величини 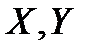 називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла інша випадкова величина.
називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла інша випадкова величина.
Математичне сподівання називають центром розподілу ймовірностей випадкової величини 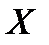 , випадкова величина
, випадкова величина  називається центрованою.
називається центрованою.
5.2. Дисперсія.
Для характеристики розсіювання значень випадкової величини відносно її центра розподілу (математичного сподівання) вводять числову характеристику – дисперсію випадкової величини. Позначається 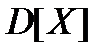 . За означенням, дисперсією випадкової величини
. За означенням, дисперсією випадкової величини 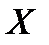 називається математичне сподівання квадрату відхилення випадкової величини від її математичного сподівання
називається математичне сподівання квадрату відхилення випадкової величини від її математичного сподівання
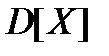 =
= 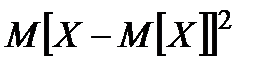 . (3)
. (3)
Дисперсія обчислюється за формулами
 =
=  (4)
(4)
для дискретних випадкових величин, і
 =
= 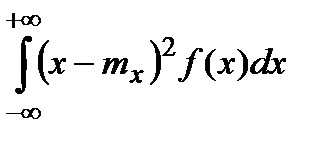 (5)
(5)
для неперервних випадкових величин. Тут для простоти позначено 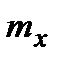 =
=  .
.
Найпростіші властивості:
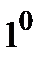 .
. 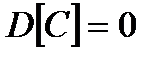 ; де
; де  - стала величина,
- стала величина,
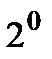 .
. 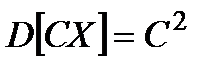
 ;
;
 .
. 
 +
+ 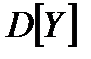 ; якщо випадкові величини
; якщо випадкові величини 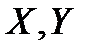 незалежні.
незалежні.
Практично дисперсію обчислюють за робочою формулою
 =
= 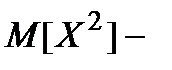
 , (6)
, (6)
де 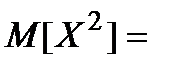
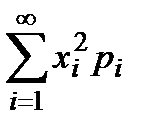 для дискретних випадкових величин і
для дискретних випадкових величин і

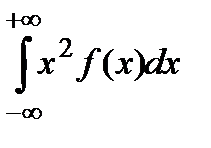 для неперервних випадкових величин.
для неперервних випадкових величин.
Дисперсія є кількісною оцінкою відхилення випадкової величини від її математичного сподівання. Проте, оскільки дисперсія має розмірність квадрата випадкової величини, то для оцінки міри розсіювання використовують характеристику 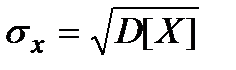 , яка називається середнім квадратичним або стандартним відхиленням випадкової величини. Оскільки
, яка називається середнім квадратичним або стандартним відхиленням випадкової величини. Оскільки 
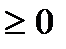 , то і
, то і
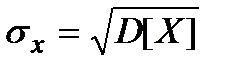
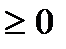 . Розмірність середнього квадратичного відхилення співпадає з розмірністю випадкової величини.
. Розмірність середнього квадратичного відхилення співпадає з розмірністю випадкової величини.
Приклад 1. Дискретна випадкова величина 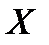 задана рядом розподілу
задана рядом розподілу
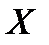
| |||||

| 0,1 | 0,2 | 0,35 | 0,20 | 0,15 |
Знайти 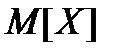 і
і  .
.
Розв’язання. За формулою (1) 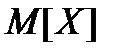 =
= 
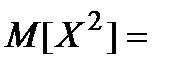
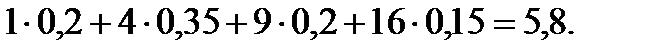
За формулою (6)  =
= 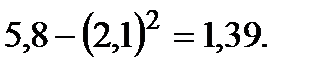 Звідки
Звідки 
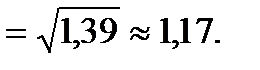
Приклад 2. Неперервна випадкова величина задана щільністю розподілу
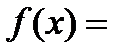

Знайти  і
і  .
.
Розв’язання. За формулою (2)  =
= 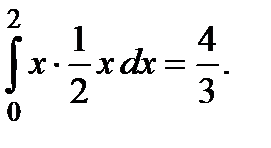
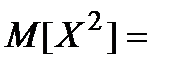
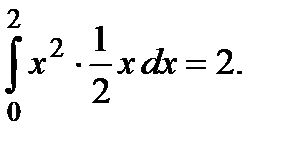
Отже, 
 =
= 
 =
= 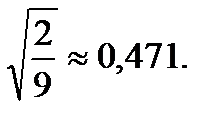
5.3. Моменти.
Більш загальною формою числових характеристик випадкових величин є моменти 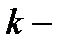 го порядку. Моментом
го порядку. Моментом 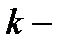 го порядку випадкової величини
го порядку випадкової величини  називається математичне сподівання
називається математичне сподівання 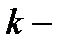 го степеня відхилення випадкової величини від деякої сталої величини
го степеня відхилення випадкової величини від деякої сталої величини 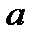
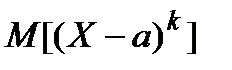 . (7)
. (7)
Якщо 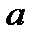 =0, то момент називається початковим
=0, то момент називається початковим 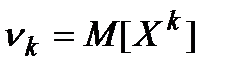 . (8)
. (8)
Очевидно, що 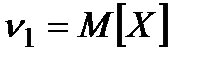 ,
, 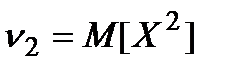 .
.
Якщо 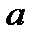 =
= 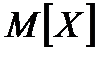 , то момент називається центральним
, то момент називається центральним 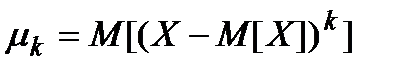 . (9)
. (9)
Очевидно, що 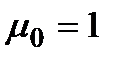 ,
, 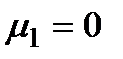 ,
, 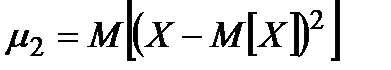 =
=  .
.
Між центральними і початковими моментами існує простий зв’язок, зокрема
 ,
, 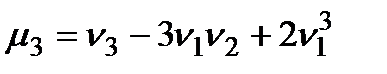 ,
,  .
.
Величина  називається абсолютним моментом
називається абсолютним моментом 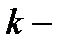 го порядку.
го порядку.
В теорії ймовірностей та її застосуваннях часто використовують інші числові характеристики.
Модою випадкової величини  (позначається
(позначається 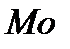 ) називається найімовірнісне значення випадкової величини.
) називається найімовірнісне значення випадкової величини.
Медіана (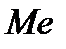 ) випадкової величини – таке значення випадкової величини, відносно якого рівноймовірно одержання більшого або меншого значення випадкової величини, тобто
) випадкової величини – таке значення випадкової величини, відносно якого рівноймовірно одержання більшого або меншого значення випадкової величини, тобто
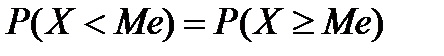 .
.
Медіана – це абсциса точки, в якій площа під кривою розподілу ділиться навпіл. Медіана визначається як корінь рівняння 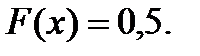
Коефіцієнт асиметрії (зкошеності)  характеризує асиметрію графіка функції розподілу.
характеризує асиметрію графіка функції розподілу.
Коефіцієнт ексцесу 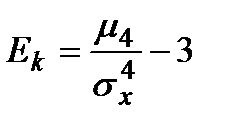 характеризує гостровершинність кривої розподілу.
характеризує гостровершинність кривої розподілу.
На практиці використовується відносна характеристика розсіювання, яка називається коефіцієнтом варіації і представляє собою середнє квадратичне відхилення у відсотках до математичного сподівання
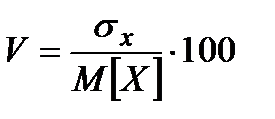 %.
%.
Коефіцієнт варіації показує, наскільки велике розсіювання порівняно із середнім значенням випадкової величини.
5.4. Числові характеристики основних законів розподілу.
Розглянемо, як обчислюються числові характеристики основних законів розподілу дискретних і неперервних випадкових величин.
Біномний розподіл.
Випадкова величина 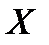 - число появ деякої події
- число появ деякої події  в
в  незалежних спробах, причому
незалежних спробах, причому  . Нехай
. Нехай  - число появ події
- число появ події  в
в 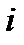 -й спробі
-й спробі  . Кожна з дискретних випадкових величин
. Кожна з дискретних випадкових величин  приймає тільки два можливі значення: 0 і 1. Отже, ряд розподілу
приймає тільки два можливі значення: 0 і 1. Отже, ряд розподілу

| ||

| 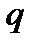
| 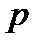
|
Звідки 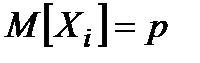 ,
, 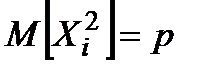 ,
, 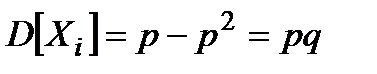 .
.
Випадкова величина 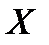 =
=  +
+ 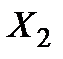 +…+
+…+ 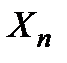 . Оскільки випадкові величини
. Оскільки випадкові величини  незалежні в сукупності, то
незалежні в сукупності, то 
 ,
, 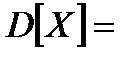
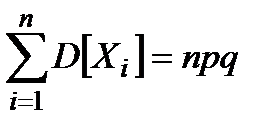 . (10)
. (10)
5.4.2. Розподіл Пуассона.
Випадкова величина Х називається розподіленою за законом Пуассона з параметром 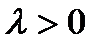 (
( пр), якщо вона приймає значення
пр), якщо вона приймає значення 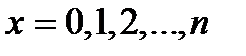 ,.. із ймовірностями
,.. із ймовірностями 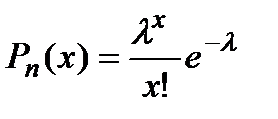 , причому
, причому 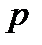 дуже мале, а
дуже мале, а  дуже велике число.!
дуже велике число.!

 =
= 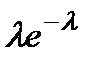
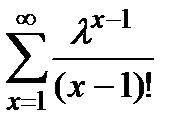 =
= 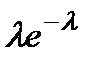
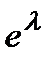 =
= 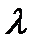 . Отже,
. Отже, 
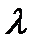 . (11)
. (11) 
 =
= 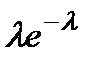
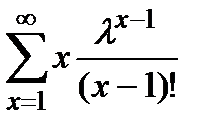 =
= 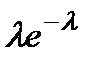
 =
= 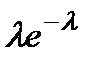
 + +
+ + 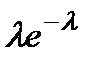
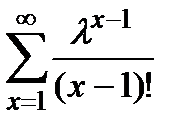 =
= 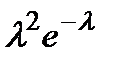
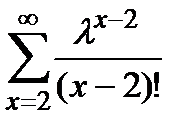 +
+ 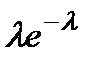
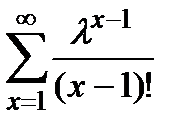 =
=  +
+ 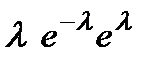 =
= 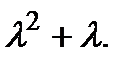
Отже,  =
=  (12)
(12)
5.4.3. Геометричний розподіл.
Ряд розподілу випадкової величини Х:
| Х | … | n | … | |||
| Р | p | qp | 
| … | 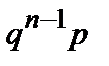
| … |
Обчислимо математичне сподівання
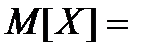
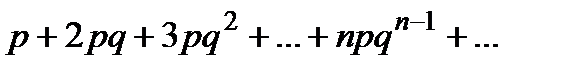 =
= 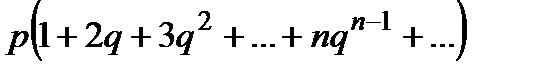 . (13)
. (13)
Для знаходження суми ряду в правій частині (13) використаємо геометричний ряд
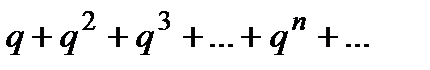 ,
, 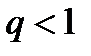
сума якого  . (14)
. (14)
Диференціюємо (14) по 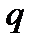 :
: 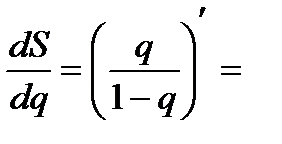

Оскільки 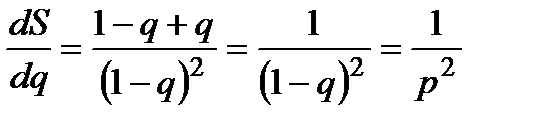 ,
, 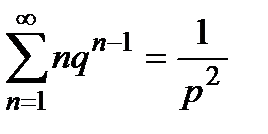 ,
,
то 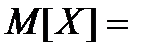
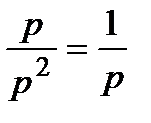 . (15)
. (15)
Знайдемо 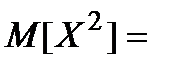
 =
= 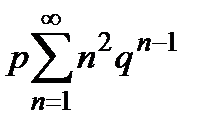 . (16)
. (16)
Ряд 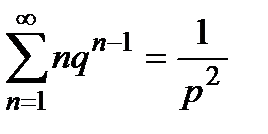 домножимо на
домножимо на 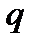 :
: 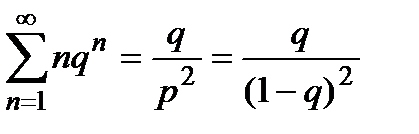 і диференціюємо по
і диференціюємо по 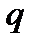
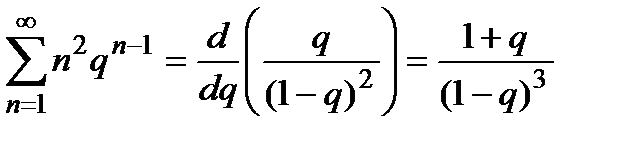 . Отриманий ряд домножимо на
. Отриманий ряд домножимо на  : звідки
: звідки 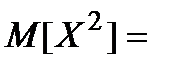
 .
.
Отже, 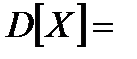

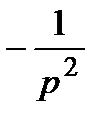 =
= 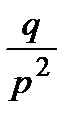 . (17)
. (17)
 2018-01-21
2018-01-21 1810
1810








