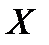
| ||||
| Р | 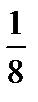
| 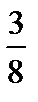
| 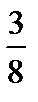
| 
|
Закон розподілу неперервної випадкової величини може бути заданий графічно або аналітично 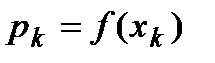 (з допомогою формули). Табличне задання неможливе, оскільки ймовірність отримати будь-яке певне значення неперервної величини дорівнює нулеві, що пов’язане не з неможливістю самої події (попадання в певну точку на числовій осі), а з безмежно великим числом можливих випадків.
(з допомогою формули). Табличне задання неможливе, оскільки ймовірність отримати будь-яке певне значення неперервної величини дорівнює нулеві, що пов’язане не з неможливістю самої події (попадання в певну точку на числовій осі), а з безмежно великим числом можливих випадків.
Тому для неперервних випадкових величин (як, зрештою, і для дискретних) визначають ймовірність попадання в деякий інтервал числової осі.
Ймовірність попадання випадкової величини 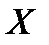 в інтервал
в інтервал 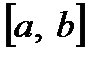 визначають як ймовірність події
визначають як ймовірність події 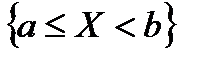
і позначають

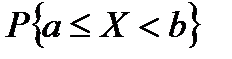 , (2)
, (2)
(ліву межу інтервалу включають, а праву не включають).
4.5. Приклади основних законів розподілу:
а) дискретних випадкових величин:
1. біномний розподіл: випадкова величина Х називається розподіленою за біномним законом, якщо вона приймає значення 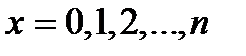 із ймовірностями
із ймовірностями
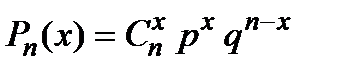 .
.
Функція розподілу 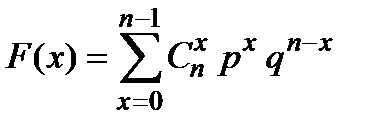 . Очевидно, що
. Очевидно, що 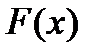 =0 при
=0 при 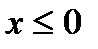 і
і 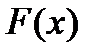 =1 при
=1 при 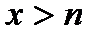 .
.
2. розподіл Пуассона: випадкова величина Х називається розподіленою за законом Пуассона з параметром 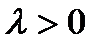 (
( пр), якщо вона приймає значення
пр), якщо вона приймає значення 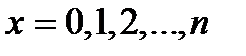 із ймовірностями
із ймовірностями 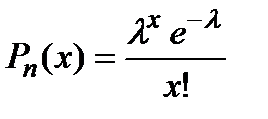 , причому
, причому 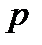 дуже мале, а
дуже мале, а  дуже велике число.
дуже велике число.
Функція розподілу 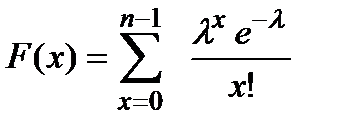 .
.
3. геометричний розподіл:
Нехай проводиться серія незалежних дослідів, в кожному з яких подія А може з’явитися з
деякою ймовірністю р. Досліди продовжуються до першої появи події А, після чого дослід припиняється.
Нехай випадкова величина Х – кількість проведених дослідів до першої появи події А.
Можливі значення величини Х: 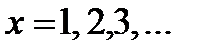 . Подія
. Подія 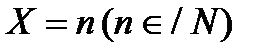 означає, що в перших
означає, що в перших 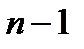 дослідах подія А не наступила, а в
дослідах подія А не наступила, а в 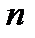 -му досліді наступила. Ймовірність
-му досліді наступила. Ймовірність 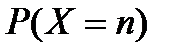 дорівнює
дорівнює
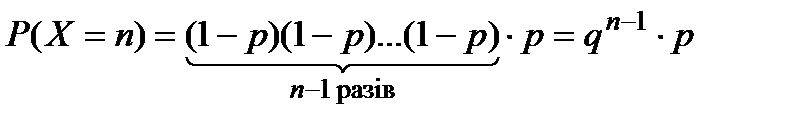

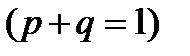 .
.
Отже закон розподілу величини Х є таким
| Х | … | n | … | |||
| Р | p | qp | 
| … | 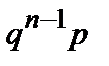
| … |
Цей розподіл називається геометричним.
Очевидно, що 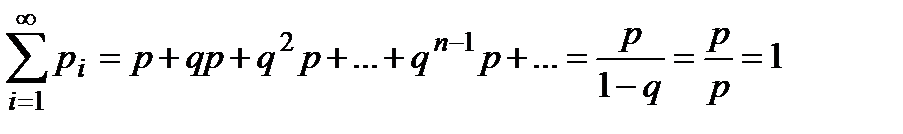 ,
,
як сума нескінченно спадної геометричної прогресії.
Функція розподілу 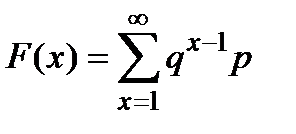 .
. 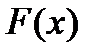 =0 при
=0 при 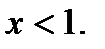
б) неперервних випадкових величин.
4. рівномірний розподіл: випадкова величина Х називається розподіленою рівномірно на інтервалі 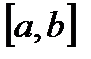 , якщо її щільність розподілу стала на цьому інтервалі
, якщо її щільність розподілу стала на цьому інтервалі
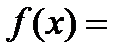
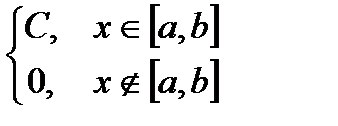
Використовуючи властивість щільності розподілу, знайдемо 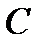 :
:
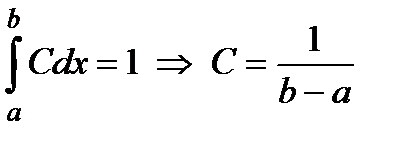 .
.
Легко бачити, що 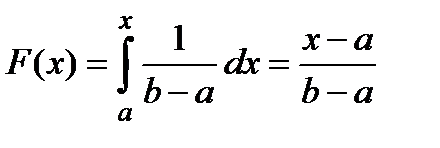 для
для 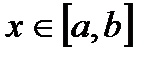 .
.
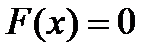 для
для 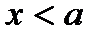 ,
, 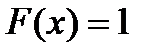 для
для 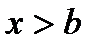
5. показниковий розподіл: випадкова величина Х називається розподіленою за показниковим (експоненційним) законом з параметром 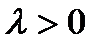 , якщо її щільність розподілу
, якщо її щільність розподілу
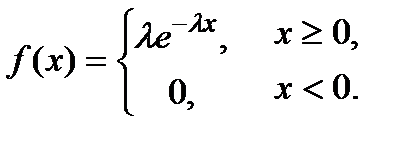
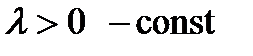
Використовуючи формулу (6) 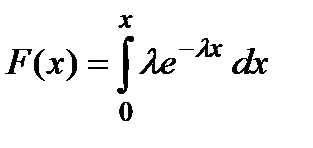 , отримаємо вираз для функції розподілу
, отримаємо вираз для функції розподілу
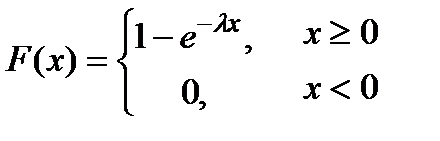 .
.
6. нормальний розподіл: випадкова величина Х називається розподіленою за нормальним законом з параметрами 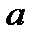 і
і  , якщо її щільність розподілу
, якщо її щільність розподілу
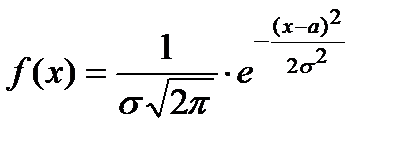 ,
, 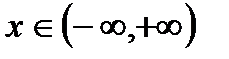 .
.
Функція розподілу має вигляд 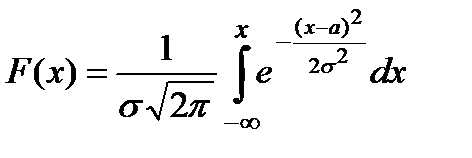 .
.
Якщо зробити заміну 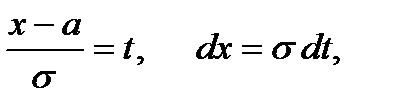
то 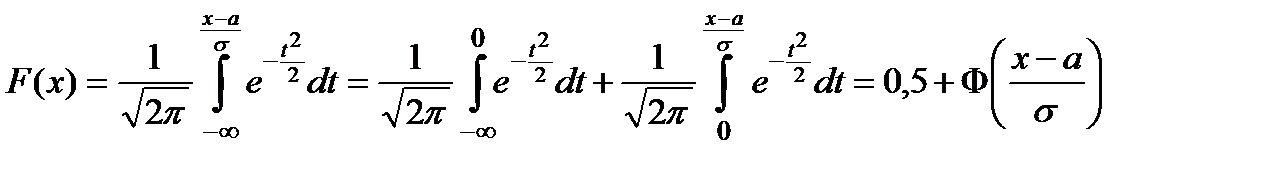 ,
,
де 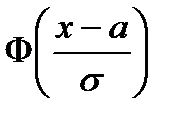 - функція Лапласа.
- функція Лапласа.
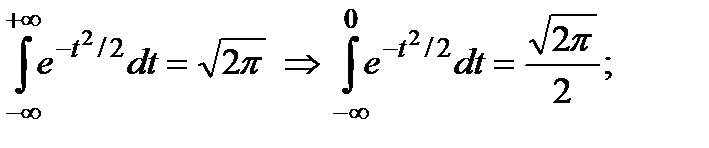
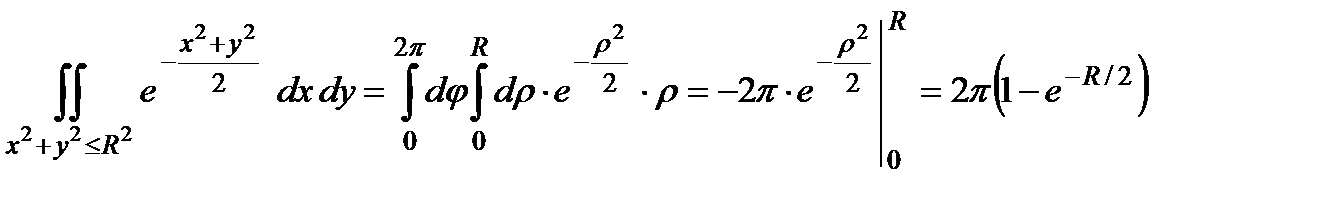 ;
;
якщо 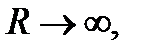 то
то 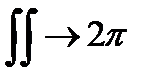 ,
,
але
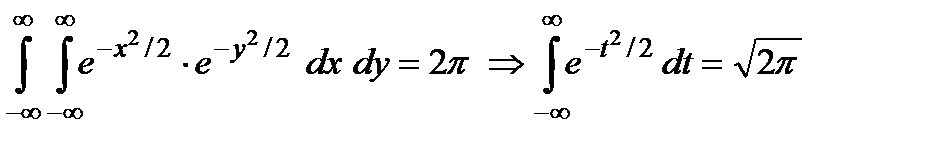 .
.
Ймовірність того, що нормально розподілена випадкова величина набуде значення з інтервалу 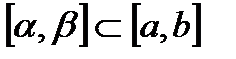 , обчислюється за формулою
, обчислюється за формулою
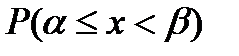 =
= 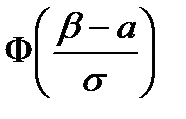
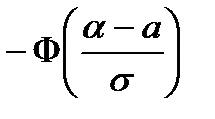 .
.
 2018-01-21
2018-01-21 674
674








