Пусть решается задача минимизации с функциональным ограничением, представленная в виде:
f(x) 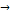 min gi
min gi 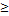 bi, F(x)
bi, F(x) 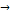 min hi=
min hi= 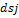 .
.
Методы штрафных функций осуществляют переход от исходной целевой функции f(x) к целевой функции следующего вида: F(x)=f(x)+ 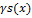 , где s(x)- штрафная функция или функция штрафа.
, где s(x)- штрафная функция или функция штрафа.
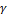 - коэффициент штрафа, который может быть постоянным или меняться в процессе оптимизации. В результате происходит переход от задачи с ограничениями к задачи безусловной оптимизации с целевой функцией F(x).
- коэффициент штрафа, который может быть постоянным или меняться в процессе оптимизации. В результате происходит переход от задачи с ограничениями к задачи безусловной оптимизации с целевой функцией F(x).
При этом штрафная функция строится таким образом, чтобы при нарушении ограничения осуществлялся штраф.
Штраф осуществляется в том, что к целевой функции прибавляется положительное число, отбрасывая оптимизационный процесс от оптимальной точки.
Существует 2 способа построения штрафных функций:
1) Метод внутренних штрафных функций. Предназначен для учета только ограничений-неравенств. При этом штрафная функция имеет вид: s(x)=1/ 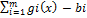 . При использовании этого метода поиск начинается с допустимой точки внутренней области, то есть точки, в которой все ограничения выполняются как строгие неравенства. При выходе на границу допустимой области значение штрафной функции будет стремится к бесконечности. Следовательно оптимизационный процесс не выйдет за пределы допустимой области. Данный метод не позволяет учитывать ограничения равенства, а также для его использования необходимо знать внутреннюю точку допустимой области.
. При использовании этого метода поиск начинается с допустимой точки внутренней области, то есть точки, в которой все ограничения выполняются как строгие неравенства. При выходе на границу допустимой области значение штрафной функции будет стремится к бесконечности. Следовательно оптимизационный процесс не выйдет за пределы допустимой области. Данный метод не позволяет учитывать ограничения равенства, а также для его использования необходимо знать внутреннюю точку допустимой области.
2) Метод внешних штрафных функций. Лишен недостатков предыдущего метода. Штрафные функции формируются следующим образом: s(x)= 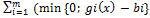 ^2+
^2+ 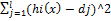 )
)
Если ограничения не нарушены, то штрафная функция равна 0. Если ограничения нарушены, то величина штрафа зависит от степени нарушения
Постановка задач векторной оптимизации. Поиск оптимально-компромиссного решения в задачах векторной оптимизации с помощью обобщенного критерия оптимальности. Способы назначения весовых коэффициентов при агрегировании частных критериев.
Задачи векторной оптимизации или задачи многокритериальной оптимизации- это задачи, в которых имеется несколько критериев оптимальности. Эти критерии образуют вектор Fi(x), i=1..n.
Все методы векторной оптимизации основаны на преобразовании задач к однокритериальной оптимизации. При этом используются 2 основных подхода:
1)Свертка локальных критериев в обобщенный показатель
2) Сведение многокритериальных задач к последовательности специальным образом сформулированных задач однокритериальной оптимизации.
Формирование обобщенного критерия оптимальности. Частные критерии оптимальности fi(x)объединяются в составной критерий F(x)=(f1(x)+f2(x)+…+fs(x)), который затем оптимизируется. При этом частные критерии должны удовлетворять следующим условиям:
1) Они должны быть соизмеримы по важности;
2) Должны быть однородными или иметь единый масштаб измерений.
С этой целью обычно проводится нормализация критерия. В качестве обобщенного критерия наиболее часто используются аддитивный критерий оптимальности F(x)= 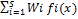 мультипликативный критерий оптимальности:F(x)=
мультипликативный критерий оптимальности:F(x)= 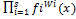 .
.
Wi весовые коэффициенты, характеризующие важность критерия. Сумма весовых коэффициентов должна быть равна 1.
Для определения весовых коэффициентов используются различные подходы:
1) Для равномерных критериев значение весовых коэффициентов определяется следующим образом: wi=1/s
2) Для неравноценных критериев весовые коэффициенты определяются в соответствии с важностью критериев. Наиболее простым является подход, который заключается в определении для каждого критерия fi(x) коэффициента относительного разброса. Весовые коэффициенты получают большее значение для тех критериев, разброс которых в допустимой области наиболее значительный.
Под оптимально-компромиссным решением понимают одну из эффективных точек, являющейся предпочтительной, с точки зрения лица, принимающего решения.
Постановка задач векторной оптимизации. Определение оптимально-компромиссного решения в мног-ных задачах на основе специальным образом сформулированных задач параметрической оптимизации. Метод главного критерия. Метод посл-ных уступок. Адаптивные алгоритмы векторной оптимизации.
При оптимизации сложных систем определить требования к объекту в виде одной целевой ф-ции бывает трудно. В этом случае оптимизацию проводят по нескольким частным критериям оптимальности: fi (х)... f$ (х), а полученная задача называет я задачами многокритериальной или векторной оптимизации. Все известные методы многокритериальной оптимизации основаны на преобразовании многокритериальной задачи в задачу с одним критерием оптимальности. При этом исп-ся 2 подхода:
1 - свёртка локальных критериев в обобщенный интегральный показатель
2 - сведение многокритериальной задачи к последовательности специальным образом сформулированных задач однокритериальной оптимизации.
Использование обобщённых критериев оптимальности часто приводит к трудностям при оптимизации, поэтому на практике часто исп-ют методы, позволяющую свести многокритериальную задачу к последовательности задач однокритериальной оптимизации. Наиболее распространёнными из них явл-ся следующие:
1) Метод главного критерия. Среди всех частных критериев fi(x) i=l,S выбирается главный
критерий ft(x). Для остальных критериев fi(x) устанавливается пороговое значение 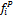 ,
,
которые не должны превышаться. При этом оптимизация производиться по главному критерию ft(x), а к системе ограничений задачи добавляется ограничение: fi(x)< 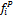 , i
, i 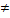 t.
t.
2) Метод последовательных уступок. Вначале критерии упорядочиваются по важности, а затем осущ-ся последовательное решение однокритериальных задач, начиная с самого важного критерия. При этом при решении каждой последующей задачи сохраняется оптимальное решение, полученное при решении предыдущих задач. При этом минимизация следующего частного критерия происходит только тогда, когда получены минимизированные значения предыдущих частных критериев. На каждом К-м шаге последовательной оптимизации вводится уступка 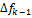 , характеризующая допустимое отклонение критерия (k-1) от его оптимального значения
, характеризующая допустимое отклонение критерия (k-1) от его оптимального значения 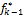 .
.
 2018-01-21
2018-01-21 1261
1261
