Задача не имеющая ограничений называются задачей безусловной оптимизации. Рассмотрим задачу безусловной оптимизации:
f(x)=F(x1..xn) -> min x  ,
,
Алгоритмы безусловной оптимизации представляют собой итерационные процедуры, реализующие последовательное приближение к искомому экстремуму.
K – номер итерации;  - направление поиска на к-ой итерации.
- направление поиска на к-ой итерации.  - величина шага в данном направлении.
- величина шага в данном направлении.
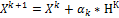
В координатной форме эта схема имеет вид:

Процесс поиска начинается с некоторой точки X0, которая называется начальным приближением и задается пользователем. По этой точке определяются точки X1 , X2 и т.д. Полученная последовательность точек называется траекторией поиска и сходится к оптимальной точке Х*. Методы безусловной оптимизации отличаются друг от друга способами выбора направления поиска  и величиной шага
и величиной шага  .
.
В зависимости от способа выбора направления поиска различают методы нулевого порядка, методы первого порядка, методы второго порядка.
Методы нулевого порядка – это методы, в которых для определения направления поиска используется только значение целевой функции. Производные при этом не используются. Они называются методами прямого поиска или поисковыми методами оптимизации.
|
|
|
Методы первого порядка – методы, в которых для определения направления поиска используются первые производные целевой функции. Эти методы называются градиентными методами оптимизации.
Методы второго порядка – это методы, в которых для определения направления поиска используются вторые производные целевой функции. К этому классу относят метод Ньютона и его модификации.
Методы второго порядка используют как первые так и вторые производные целевой функции. К этому классу относят метод Ньютона и его модификации, которые строятся по следующей схеме:

Где 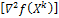 - матрица вторых производных целевой функции.
- матрица вторых производных целевой функции.
Данные методы отличаются друг от друга способом выбора шага. В классическом методе ньютона шаг равен 1 на всех итерациях.
В методе Ньютона- Равсона шаг перестраивается в процессе оптимизации, при этом используется 2 способа выбора шага:
1) Связан с проверкой условия  и дробление шага в случае его невыполнения
и дробление шага в случае его невыполнения
2) Связан с определением на каждой итерации оптимальной длины шага, в результате решения вспомогательной задачи одномерной оптимизации: min (F(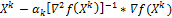 )).
)).
 2018-01-21
2018-01-21 1491
1491
