Среднее арифметическое (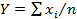 , my=mx, D(y)=D(x)/n) случ величины Х есть случ величина с очень маленькой дисперсией и при достаточно большомn ведет себя как не случ.
, my=mx, D(y)=D(x)/n) случ величины Х есть случ величина с очень маленькой дисперсией и при достаточно большомn ведет себя как не случ.
Теорема Чебышева:
При достаточно большом числе независимых опытов, среденее арифметическое наблюдаемых значений случ величины сходится по вероятности к ее mх.
P(|xn-a|<ε)>1-δ, ε, δ -> 0.
P(|(∑xi/n) - mx|<ε)>1-δ
Д-во:
Y=∑xi/n, my=mx, Dy=Dx/n.
Применим к случ величине Y неравенство Чебышёва.
P(|y-my|≥ε)≤Dy/ε²=Dx/nε².
P(|(∑xi/n)-mx|≥ε)≤δ
P(|(∑xi/n)-mx|<ε)>1-δ
Теорема Бернулли (об устойчивости частот) (доказать).
Если вероятностьпоявления события А в одном испытании равна р, число наступления
этого события при п независимых испытаниях равно na, то для любого числа £ > 0 имеет место равенство
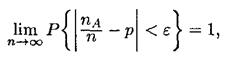
т.е. относительная частота Р*(A) события А сходится по вероятности крвероятности события 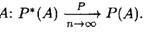
Док-во:
QВведем с. в. Х1, Х2,...,Хп следующим образом: Хi = 1, если в i-м испытании появилось событие А, а если не появилось, то Xi= 0. Тогдачисло пд (число успехов) можно представить в виде
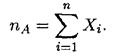
М.о. и дисперсия с. в. Xiравны: MXi= 1 • р + 0 • (1 — р) = р
DXi~ (0 — р)2(1 — р) + (1 — р)2р = р(1 —р)= pq
Закон распределения
с. в. Xiимеет вид
| Xi | ||
| р | 1 -р | рi |
при любом». Таким образом, с. в. Хi независимы, их дисперсии ограничены одним и тем же числом так как
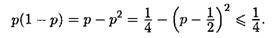
Поэтому к этим с. в. можно применить теорему Чебышева (5-7):
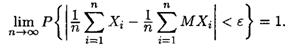 но
но 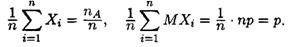
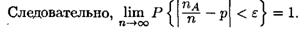
 2018-01-21
2018-01-21 822
822








