Умножение вектора на число

Опр. 10. Произведением вектора на скаляр k называется вектор

= k = k,

имеющий длину ka, и направление, которого:

1. совпадает с направлением вектора , если k > 0;

2. противоположно направлению вектора , если k < 0;

3. произвольно, если k = 0.

Свойства умножения вектора на число.

1^о. (k + l) = k + l .

k ( + ) = k + k .

2^o. k (l ) = (kl) .

3^o. 1× = , (–1) × = – , 0 × = .

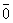Свойства векторов.

Опр. 11. Два вектора и называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.

Нулевой вектор коллинеарен любому вектору.

Теорема 1. Два ненулевых вектора и коллинеарны, Û когда они пропорциональны т.е.

= k , k – скаляр.

Опр. 12. Три вектора , , называются компланарными, если они параллельны некоторой плоскости или лежат в ней.

Теорема 2. Три ненулевых вектора , , компланарны, Û когда один из них является линейной комбинацией двух других, т.е.

= k + l , k,l – скаляры.

Проекция вектора на ось.

Теорема 3. Проекция вектора на ось (направленная прямая) l равна произведению длины вектора на косинус угла между направлением вектора и направлением оси, т.е. = a × c os a, a = Ð( , l).

рис.3.

КООРДИНАТЫ ВЕКТОРА

Опр. 13. Проекции вектора на координатные оси Ох, Оу, Оz называются координатами вектора. Обозначение: { a_x,a_y, a_z }.

Длина вектора:

Пример: Вычислить длину вектора .

Решение:

Расстояние между точками и вычисляется по формуле: .

Пример: Найти расстояние между точками М (2,3,-1) и К (4,5,2).