Даны векторы  ={ ax, ay, az } и
={ ax, ay, az } и  ={ bx, by, bz }.
={ bx, by, bz }.
1. (  ±
±  )={ ax ± bx, ay ± by, az ± bz }.
)={ ax ± bx, ay ± by, az ± bz }.
2. l  = { lax, lay, laz }, где l – скаляр.
= { lax, lay, laz }, где l – скаляр.
Скалярное произведение векторов.
Определение: Под скалярным произведением двух векторов  и
и 
понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.  =
= 
 ,
,  - угол между векторами
- угол между векторами  и
и  .
.
Свойства скалярного произведения:
1.  ×
×  =
= 

2. (  +
+  )
)  =
= 
3. 
4. 
5.  , где
, где  – скаляры.
– скаляры.
6. два вектора перпендикулярны (ортогональны), если  .
.
7. 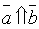 тогда и только тогда, когда
тогда и только тогда, когда 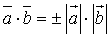 .
.
Скалярное произведение в координатной форме имеет вид:  , где
, где  и
и  .
.
Пример: Найти скалярное произведение векторов 
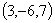 и
и 
Решение: 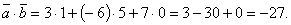
 2018-01-21
2018-01-21 310
310








