Алгоритм графического метода решения ЗЛП

1) Предположим, что система неравенств (3.1) совместна. На координатной плоскости 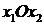построим область допустимых решений (ОДР), соответствующую системе ограничений (3.1). Каждое неравенство системы (3.1) определяет полуплоскость () с граничной прямой (). Пусть, например, полуплоскость определяется неравенством . Для построения полуплоскости () достаточно подставить в соответствующее неравенство координаты любой точки (например, (0, 0)) и проверить истинность полученного неравенства. Если неравенство истинное, то необходимо заштриховать полуплоскость, содержащую данную точку. В случае, если неравенство ложное, то заштриховать полуплоскость, не содержащую данную точку.

Рис. 3.1.

Условия неотрицательности управляющих переменных , определяют полуплоскость с граничными прямыми , (первую координатную четверть). Так как система ограничений совместна, то полуплоскости имеют общую область. Пересечение полуплоскостей является выпуклым множеством и представляет собой совокупность точек, координаты которых составляют допустимые решения.

2) Построить градиент (вектор) целевой функции :

с началом в точке и концом в точке , показывающий направление наибольшего возрастания целевой функции .

3) Построить линию уровня целевой функции . Эта линия есть прямая

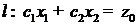
(при получаем линию нулевого уровня , см. рис. 3.1), и она перпендикулярна градиенту 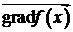. Как правило, значение 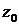целесообразно выбирать таким образом, чтобы соответствующая прямая (линия уровня) имела с ОДР по крайней мере две общие точки.

4) При решении задачи на максимум функции следует перемещать линию уровня 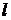в направлении градиента до тех пор, пока у нее не окажется всего одна общая точка с ОДР. Эта точка, определяющая единственное решение ЗЛП, будет точкой экстремума (максимума). При решении задачи на минимум функции следует перемещать линию уровня в направлении, противоположном направлению градиента до тех пор, пока у нее не окажется всего одна общая точка с ОДР. Эта точка, определяющая единственное решение ЗЛП, будет точкой экстремума (минимума).

5) Найти координаты вершины многоугольника, являющейся точкой экстремума. Для этого нужно решить систему уравнений тех прямых, пересечением которых является данная вершина.

6) Вычислить значение целевой функции в полученной вершине.

Замечание 3.1. Если при движении вдоль градиента 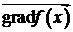линия уровня не покидает ОДР, то в этом случае ОДР является неограниченным множеством в направлении оптимизации. В этом случае условно полагают, что или .

Замечание 3.2. ЗЛП не будет иметь решений, если ОДП является пустым множеством. Это означает, что система ограничений имеет противоречивые неравенства, и на координатной плоскости нет ни одной точки, удовлетворяющей всем ограничениям сразу.

Замечание 3.3. При решении ЗЛП графическим методом может встретиться случай, когда линия уровня параллельна одной из сторон выпуклого многоугольника допустимых решений, причем эта сторона расположена в направлении оптимизации. Тогда оптимальное значение целевой функции достигается в двух угловых точках (вершинах) области допустимых решений, а, следовательно, и во всех точках отрезка, соединяющего эти вершины, то есть ЗЛП имеет бесконечное множество решений (альтернативный оптимум).

Пример 3.1. Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в таблице:

Исходный продукт	Расход исходных продуктов на 1 кг мороженого	Запас, кг
Сливочное	Шоколадное
Молоко	0,8	0,5
Наполнители	0,4	0,8

Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более, чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 руб., шоколадного – 14 руб. Какое количество мороженого каждого вида должна производить

фирма, чтобы доход от реализации продукции был максимальным? [1; 2].

Решение. Обозначим управляющие переменные: – суточный объем выпуска сливочного мороженого, кг; – суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи. Целевая функция будет иметь вид .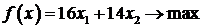

Составим неравенства для ресурсных ограничений. Ограничение по молоку имеет вид: ; по наполнителям: . Составим неравенства для рыночных ограничений по спросу. Разница в суточном спросе на 2 вида мороженого составляет . Ограничение на суточный спрос шоколадного мороженого .

Тогда математическая модель задачи будет иметь вид

Далее решим задачу графическим методом по алгоритму.

1) Построим область допустимых решений. Неравенство определяет полуплоскость, расположенную левее и ниже прямой , то есть прямой . Неравенство определяет полуплоскость, расположенную левее и ниже прямой . Ограничение определяет полуплоскость, расположенную левее и ниже прямой . Ограничение определяет полуплоскость, расположенную левее прямой , ограничения , определяют первую координатную четверть. Множество допустимых решений ЗЛП не пусто. Обозначим вершины многоугольника решений: (рис. 3.2).

Рис. 3.2.

2) Построим градиент целевой функции :

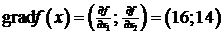3) Построим линию уровня целевой функции : . Линия уровня перпендикулярна вектору .

4) Перемещая прямую по направлению параллельно самой себе, найдем предельную точку, в которой целевая функция покинет область допустимых решений (пунктирная линия на рис. 3.2). Предельная точка многоугольника – точка .