1. Привести систему ограничений канонической ЗЛП к допустимому виду. Выделить базис переменных. Соответствующим образом записать целевую функцию ЗЛП (она должна зависеть от свободных переменных).
2. Построить начальный опорный план (базисное решение) и найти значение целевой функции на начальном опорном плане.
3. Проверить выполнимость условия теоремы 5.1. Если условие теоремы 5.1 выполняется (случай 1), то построенное в пункте 2 базисное решение является оптимальным. Записать ответ.
4. Если условие теоремы 5.1 не выполняется, то проверить выполнимость условий теоремы 5.2. Если условие теоремы 5.2 выполняется (случай 2), то данная ЗЛП не имеет оптимального решения. Задача решена.
5. Найти разрешающий элемент и выяснить, какая из базисных переменных выйдет из базиса, а какая свободная переменная войдет в базис. Выразить из системы ограничений допустимого вида свободную переменную через базисную переменную, соответствующим образом подставить в остальные уравнения выражение для свободной переменной. Изменить целевую функцию (она должна зависеть от свободных переменных). Получить таким образом новую ЗЛП допустимого вида с новой системой ограничений и целевой функцией. Перейти к пункту 2.
Пример 5.3. Найти оптимальное решениеЗЛП допустимого вида
 (
( ),
),

Решение. В данном случае система ограничений имеет допустимый вид,  ,
,  , базисное решение
, базисное решение  .
.
Перепишем систему ограничений в виде

Введем целевую функцию 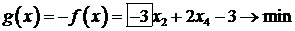 . Значение целевой функции
. Значение целевой функции 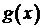 на базисном решении равно
на базисном решении равно  .
.
Заметим, что условия теорем 5.1 и 5.2 не выполняются, значит, имеем случай 3. В целевой функции 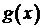 при свободной переменной
при свободной переменной  стоит отрицательный коэффициент (
стоит отрицательный коэффициент ( ), а в системе ограничений при этой же переменной стоят два отрицательных коэффициента:
), а в системе ограничений при этой же переменной стоят два отрицательных коэффициента: 
 (случай 3.2). Составим вспомогательное число
(случай 3.2). Составим вспомогательное число
 .
.
Разрешающим элементом является элемент  (он выделен в прямоугольник). Тогда необходимо изменить базис переменных:
(он выделен в прямоугольник). Тогда необходимо изменить базис переменных:  . Для этого из системы ограничений допустимого вида необходимо выразить переменную
. Для этого из системы ограничений допустимого вида необходимо выразить переменную  через переменную
через переменную  . Получим
. Получим
 .
.
Подставляя в систему ограничений вместо переменной  полученное выражение, получим новую систему ограничений
полученное выражение, получим новую систему ограничений
 Соответствующим образом изменим целевую функцию
Соответствующим образом изменим целевую функцию
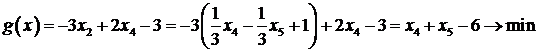 .
.
Итак, получаем новую ЗЛП допустимого вида

 (
( ).
).
В новой ЗЛП 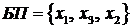 ,
,  . Построим базисное решение
. Построим базисное решение  . Значение целевой функции на базисном решении
. Значение целевой функции на базисном решении 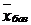 равно
равно  . Так как в целевой функции
. Так как в целевой функции  все коэффициенты при свободных переменных неотрицательны, то согласно теореме 4.1 базисное решение
все коэффициенты при свободных переменных неотрицательны, то согласно теореме 4.1 базисное решение  является оптимальным. При этом
является оптимальным. При этом  , а тогда
, а тогда  . Итак,
. Итак,
 ,
, 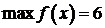 .
.
 2018-01-21
2018-01-21 646
646








