Формы записи ЗЛП, их эквивалентность и способы преобразования

Задачу линейного программирования можно записать в одной из приведенных ниже форм.

Общая форма записи:

,

произвольного знака .

Симметрическая (стандартная) форма записи:

,

,

Каноническая форма записи:

,

.

Указанные формы записи ЗЛП эквивалентны в том смысле, что в результате некоторых преобразований можно перейти от одной формы записи к другой. Если имеется способ нахождения оптимального решения ЗЛП, записанной в одной форме, то можно определить и оптимальное решение ЗЛП, записанной в другой форме.

Замечание 1.1. Задачу максимизации целевой функции можно заменить задачей минимизации:

.

Замечание 1.2. Неравенство типа можно заменить на неравенство типа путем умножения обеих частей этого неравенства на число .

Замечание 1.3. Ограничение-неравенство вида

преобразуется в ограничение-равенство путем введения так называемой балансовой неотрицательной переменной :

.

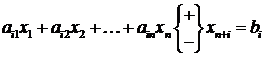Рассмотрим на примерах способы перехода от одной формы записи ЗЛП к другой форме записи.

Пример 1.1. Привести к канонической форме записи ЗЛП:

,

.

Решение. ЗЛП представлена в общей форме записи. Для сведения ее к канонической форме в первое и третье ограничения-неравенства введем балансовые переменные 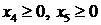. Изменим также тип экстремума, введя целевую функцию . Тогда

,

Пример 1.2. Привести к симметрической форме записи ЗЛП

,

.

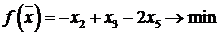Решение. ЗЛП представлена в канонической форме записи. Для сведения ее к симметрической форме записи исключим (выразим) три переменные через остальные переменные. В данном случае удобно выразить переменные через , и учесть условие их неотрицательности:

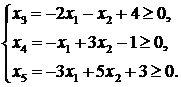
Опустив переменные , придем к эквивалентным неравенствам. Для получения целевой функции симметрической задачи необходимо вместо переменных подставить выражения из последней системы в исходную целевую функцию

.

В результате получаем симметрическую ЗЛП

,

.

§ 2. Математические модели экономико-математических задач

В данном параграфе рассмотрим несколько примеров задач линейного программирования, к которым приводятся математические модели реальных экономических задач.

Пример 2.1 (задача о банке). Пусть собственные средства банка в сумме с депозитами состав­ляют 100 млн долл. Часть этих средств, но не менее 35 млн долл. должна быть размещена в кредитах. Кредиты являются неликвид­ными активами банка, так как в случае непредвиденной потреб­ности в наличности обратить кредиты в деньги без существенных потерь невозможно. Другое дело ценные бумаги, особенно государственные. Их можно в любой момент продать, получив некоторую прибыль или, во всяком случае, без большого убытка. Поэтому существует пра­вило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы – ценные бумаги, чтобы компенсировать неликвидность кредитов. В нашем приме­ре ликвидное ограничение таково: ценные бумаги должны состав­лять не менее 30% средств, размещенных в кредитах и ценных бумагах.

Обозначим через 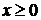– средства (млн долл.), размещенные в кредитах, – средства, вложенные в ценные бумаги. Согласно условию задачи имеем следующую систему линейных ограничений:

В этой системе ограничений неравенство (1) означает балансовое ограничение, неравенство (2) означает кредитное ограничение, неравенство (3) - ликвидное ограничение. Цель банка состоит в том, чтобы получить максиальную прибыль от кредитов и ценных бумаг. В результате получаем целевую функцию (функцию прибыли банка)

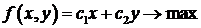, (4)

где c₁ – доходность кредитов, с₂ – доходность ценных бумаг, причем так как кредиты менее ликвидны, чем ценные бумаги, то обычно полагают c₁ > с₂.

Итак, получена задача линейного программирования с ограни­чениями (1) – (3) и целевой функцией (4), которую требуется максими­зировать.

Пример 2.2 (задача об использовании ресурсов). Предприятие имеет в своем распоряжении определенное количество ресурсов: рабочую силу, деньги, сырье, оборудование, производственные ресурсы, площади и т.п. Допустим, что ресурсы трех видов имеются в количестве соответственно условных единиц. Предприятие выпускает три вида товаров . Причем известно, сколько единиц каждого ресурса требуется для производства единицы каждого товара. Пусть – число единиц ресурса R_i (i= 1, 2, 3), необходимое для производства единицы товара (j =1, 2, 3). Доход, получаемый предприятием от единицы каждого вида товаров, соответственно равен 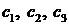. Требуется при данных ресурсах выпустить такую комби­нацию товаров, при которой доход предприятия будет макси­мальным.

Обозначим через соответственно количество товаров . При этом доход предприятия выражается функцией

.

Общее количество ресурса (i= 1, 2, 3), используемого при выпуске товара 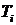(i= 1, 2, 3), равно . Оно не должно превосходить

запаса (i= 1, 2, 3), то есть

.

Тогда математическая задача об использовании ресурсов состоит в определении неотрицательных значений , удовлетворяющих системе

и максимизирующих целевую функцию дохода .

Пример 2.3 (транспортная задача). Уголь, добываемый в нескольких месторождениях, отправляется потребителям: заводам, электростанциям и т.п. Известно, сколько угля добывается в каждом из месторождений, и сколько его требуется каждому из потребителей; расстояния между месторождениями и потребителями, а также условия сообщения между ними. В результате можно подсчитать, во что обходится перевозка каждой тонны угля из любого месторождения в любой пункт потребления. Требуется, при этих условиях спланировать перевозки угля таким образом, чтобы затраты были минимальными.

Предположим для определенности, что имеются два месторождения и три потребителя . Количество угля в месторождениях равны соответственно 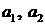. Запросы потребителей равны соответственно . Считаем, что суммарные запасы равны суммарным потребностям (так называемое условие сбалансированности):

.

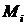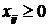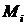Наконец, заданы числа (), представляющие собой стоимость перевозки тонны угля из месторождения () поставщику (). При этом необходимо определить шесть неотрицательных чисел (), где количество угля, предназначенное к отправке из () к (). Составим таблицу:

				Всего отправлено
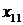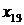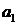Всего доставлено

Общее количество угля, вывезенное из месторождения 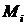() должно равняться (). Отсюда имеем условие

().

Общее количество угля, доставленное потребителю () должно равняться (). Отсюда имеем условие

().

Предполагается, что затраты на перевозку прямо пропорциональны количеству перевозимого угля, то есть перевозка из 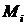() в () стоит . Тогда общие затраты по всем перевозкам будут

.

Таким образом, приходим к следующей задаче линейного программирования, которую называют транспортной задачей линейного программирования (ТЗЛП):

,

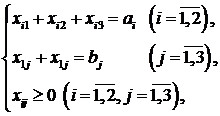
Заметим, что ТЗЛП – это особая задача линейного программирования, для решения которой (для нахождения оптимального плана перевозок) применяются специальные методы. Подробно с методами решения ТЗЛП мы познакомимся в главе 2.