Дистилляция многокомпонентных смесей

Однократная непрерывная дистилляция многокомпонентных смесей производится также как и для бинарных смесей (разд. 14.1.2.1). Схема установки изображена на рис. 14.35.

 

 

Рис. 14.35. Схема установки непрерывной однократной многокомпонентной дистилляции: 1 испаритель; 2 сепаратор; 3 конденсатор

 

Запишем для нее систему уравнений материального (молярного) баланса, как для смеси в целом, так и для всех компонентов, за исключением, наименее летучего n:

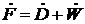(14.80)

(14.81)

где мольные расходы исходной смеси, дистиллята и кубового остатка; составы соответствующих смесей в мольных долях.

Так как удаляющийся пар находится в равновесии с кубовым остатком и при полной конденсации пара его состав и состав дистиллята одинаковы, то систему уравнений (14.80) и (14.81) можно дополнить уравнениями равновесия:

(14.82)

где матрица-столбец .

С использованием доли отгона (доли отбора дистиллята) е, систему уравнении (14.80) – (14.82) можно преобразовать следующим образом: выразим 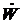из (14.80), подставим в (14.81), поделим на 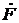, вместо подставим (14.82) и решим относительно

,

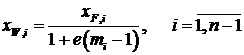, (14.83)

. (14.84)

Следуя приближению (12.52), справедливому для умеренных давлений, можно записать:

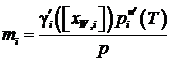, (14.85)

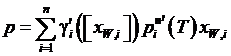. (14.86)

В соответствии с правилом фаз Гиббса для двухфазной,
n- компонентной системы число независимых переменных равно n:

С = n – Ф + 2 = n – 2 + 2 = n. (14.87)

В качестве независимых переменных могут быть p, x_{W , i}, ; тогда заданными величинами будут являться p, [ x_{F , i} ], e, а неизвестными будут T, x_{D , i}, x_{W , i}, m_i, 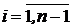, которые находятся из решения 3(n –1)+1 уравнений системы (14.82) – (14.86).

Могут задаваться известными величинами давление и температура дистилляции. В этом случае температура является заданной величиной, а доля отгона е находится из решения системы уравнении (14.82) – (14.86). В качестве известных величин могут рассматриваться давление и концентрация ключевого компонента в дистилляте x_{D ,1} или в кубовом остатке x_{W ,1}, тогда доля отгона и температура определяются также из решения системы уравнений
(14.82) – (14.86). Следует иметь в виду, что температура и концентрация ключевого компонента не могут задаваться произвольными значениями. Они должны соответствовать диапазону изменения доли отгона , поэтому предварительно необходимо решить задачу в первой постановке при e = 0 и е =1, чтобы определить интервал изменения T, x_{D ,1}, x_{W ,1}.

Постепенная периодическая многокомпонентная дистилляция проводится аналогично бинарной (разд. 14.1.2.3). Схема установки изображена на рис. 14.36.

 

Рис. 14.36. Схема установки постепенной многокомпонентной дистилляции: 1 куб-испаритель; 2 конденсатор; 3 сборник дистиллята; 4 измеритель температуры

 

Запишем в дифференциальной форме уравнения материального баланса для текущего момента времени по каждому компоненту, за исключением, наименее летучего n. Количество компонента i в кубовой жидкости, то есть количество молей L с содержанием x_i за бесконечно малый промежуток времени уменьшается на dL_i = d (Lx_i). Такое же количество вещества компонента i должно перейти в пар , тогда

(14.88)

Разделив, переменные мы получим:

. (14.89)

Так как является функцией концентраций всех компонентов, то систему дифференциальных уравнении (14.89) необходимо решать совместно с уравнениями равновесия:

. (14.90)

Рассмотрим в качестве заданных величин давление р, количество F и состав исходной смеси, а также концентрацию в кубе ключевого компонента x_{W, 1} или долю отгона e, либо температуру окончания процесса T _к. Систему дифференциальных уравнений (14.89) лучше решать численно, при этом на каждом шаге интегрирования по dL определяются последовательно: приращения [ dx_i ] из уравнения (14.89), состав жидкости [ x_i ] = [ x_i (L)]+[d x_i ], температура насыщения T из (14.86) при замене x_{W , i} на x_i, коэффициенты распределения [ m_i ] из уравнения (14.85), состав удаляющегося равновесного пара , количество оставшейся кубовой жидкости L dL. Интегрирование проводится от L = F и [ x_i ] = [ x_F,i ] до достижения заданной концентрации в кубе ключевого компонента x_{W, 1} или доли отгона e, либо температуры окончания процесса T _к. Средний состав дистиллята , полученный в результате дистилляции, может быть найден из системы уравнении материального баланса аналогичной (14.80) и (14.81), при использовании F, D, W, характеризующих не расход, а количество молей исходной смеси, дистиллята и кубового остатка:

. (14.91)

Интегрирование системы уравнений (14.88) может быть произведено аналитически, если допустить неизменными коэффициент относительной летучести каждого из компонентов i по отношению к одному, например, наименее летучему n в диапазоне изменения состава куба при дистилляции. Поделим уравнение (14.88) на аналогичное уравнение для компонента n:

(14.92)

Разделим переменные и проинтегрируем:

(14.93)

или

,

с учетом того, что W = F – D, e = D/F:

,

учитывая :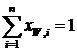

(14.94.)

При заданных доле отгона e, составе исходной смеси [ x_{F , i} ] и коэффициентах относительной летучести [a _in ] решением системы уравнений (14.94), находятся концентрации компонентов в кубовом остатке [ x_{W , i} ]. Существует другой вариант: может быть задана концентрация ключевого компонента в кубовом остатке x_{W ,1}, а доля отгона e является искомой величиной. Концентрация компонентов в дистилляте находится по уравнению (14.91).