На основі дослідів, проведених В. Фрічем, в ядрі течії градієнт швидкості залежить тільки від двох величин: динамічної швидкості u* і відстані у до стінки (від точки на кривій розподілу швидкості до стінки труби). Тобто
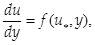 (109)
(109)
Градієнт швидкості  можна знайти скориставшись методом аналізу розмірностей. Приймаючи степеневу залежність в рівнянні (109), дістанемо
можна знайти скориставшись методом аналізу розмірностей. Приймаючи степеневу залежність в рівнянні (109), дістанемо
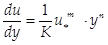 (110)
(110)
де 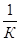 , m, n ― деякі константи.
, m, n ― деякі константи.
Запишемо рівняння (110) через розмірності:
L0 T-1 = Lm T-m Ln
З цієї рівності маємо:
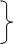 0 = m+n
0 = m+n
-1 = -m
Звідки: m = 1; n = -1.
При отриманих значеннях m і n рівняння (110) приймає вигляд:
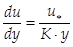 . (111)
. (111)
Тоді зміна швидкості в ядрі потоку буде
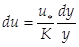 .
.
Інтегруючи це рівняння, отримаємо
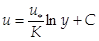 (112)
(112)
формула (112) показує, що закон розподілу швидкості в ядрі турбулентного потоку ― логарифмічний, що підтверджується експериментами.
Епюра розподілу швидкості в поперечному перерізі турбулентного потоку.
З формули (112) для циліндричної труби після певних перетворень можна дістати залежності для визначення середньої і максимальної швидкостей в ядрі турбулентного потоку, а також знайти залежність положення вектора осередненої швидкості в ядрі потоку від стінки труби до певної точки, де розташовується цей вектор.
Середня швидкість:
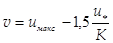 ; (113)
; (113)
вектор осередненої швидкості
ū = v +5,09 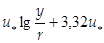 ; (114)
; (114)
вектор максимальної швидкості
ū 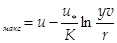 ; (115)
; (115)
yv = 0,223 r,(116)
де r – радіус труби
yv – відстань від стінки до точки, де знаходиться вектор середньої швидкості. Тоді епюра розподілу осереднених швидкостей в поперечному перерізі буде мати наступний вигляд:
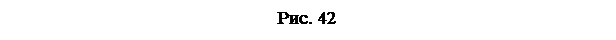
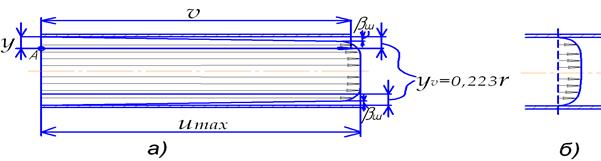
Як видно з рис. 42.а всі вектори швидкостей є осереднені. Вони розташовані паралельно осі і один одному. Тобто, як було сказано раніше, хаотичний рух частинок рідини в ядрі турбулентного потоку перетворений у фіктивно паралельно струминний рух.
В пристінному шарі зміна швидкості частинок рідини відповідає ламінарному закону. Якщо величина пристінного шару менша за висоту виступів шорсткості внутрішньої поверхні труби, то ядро турбулентного потоку займає весь переріз труби (рис. 42 б).
Втрати напору за довжиною труби при турбулентному русі рідини визначається залежністю
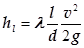 .
.
Тобто, по формі такою ж самою як і для ламінарного режиму. Але „ 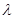 ” (коефіцієнт опору тертя за довжиною) при турбулентному режимі розраховуються за іншими закономірностями, при яких, як буде видно далі, hl буде залежати від швидкості потоку не в першій степені, тому що
” (коефіцієнт опору тертя за довжиною) при турбулентному режимі розраховуються за іншими закономірностями, при яких, як буде видно далі, hl буде залежати від швидкості потоку не в першій степені, тому що  , як показують досліди, є величина, яка в першу чергу залежить від матеріалу і стану внутрішньої поверхні труби, а також від співвідношення еквівалентної шорсткості Dекв внутрішньої поверхні, діаметра труби величини пристінного шару
, як показують досліди, є величина, яка в першу чергу залежить від матеріалу і стану внутрішньої поверхні труби, а також від співвідношення еквівалентної шорсткості Dекв внутрішньої поверхні, діаметра труби величини пристінного шару  , який, в свою чергу, змінюється від зміни швидкості руху рідини.
, який, в свою чергу, змінюється від зміни швидкості руху рідини.
Шорсткість може бути рівномірно-зернистою, рівномірно-хвилястою, нерівномірно-зернистою, нерівномірно-хвилястою. До того ж вона характеризується не тільки розмірами, а й формою виступів.
Тому за розрахункову шорсткість беруть не середню абсолютну величину виступів D, а так звану еквівалентну шорсткість, яка приводиться у відповідних довідниках Dекв. ця величина не заміряється, а одержується гідравлічним способом на дослідній установці для квадратичної зони гідравлічних опорів.
Еквівалентною шорсткістю називається така уявна подібна до рівномірно – зернистої шорсткості, однакова по всій довжині трубопроводу, при якій втрати напору на одиницю довжини будуть такими ж самими, як і при дійсній шорсткості.
З метою визначення коефіцієнта опору тертя за довжиною при турбулентному русі розглянемо так звані зони гідравлічних опорів.
Перша зона – зона гідравлічно гладких труб. Ця зона відбувається при малих числах Re, яким відповідає саме більше значення пристінного шару. При цьому пристінний шар покриває виступи шорсткості, тобто 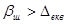 (рис.43. 1).
(рис.43. 1).
З одного боку 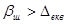 , а з другого
, а з другого 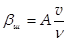 . з цієї нерівності
. з цієї нерівності 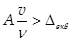 випливає, що сиплекс
випливає, що сиплекс 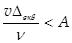 . дослідами встановлено, що для гідравлічно-гладкої зони гідравлічних опорів А = 63. звідси, якщо симплекс
. дослідами встановлено, що для гідравлічно-гладкої зони гідравлічних опорів А = 63. звідси, якщо симплекс 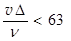 , то внутрішня поверхня труби – гідравлічно-гладка, для якої характерно
, то внутрішня поверхня труби – гідравлічно-гладка, для якої характерно 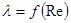 . Ця залежність визначаються рядом формул:
. Ця залежність визначаються рядом формул:
а) 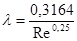 - формула Стокса (рекомендується для випадків коли Re <105)
- формула Стокса (рекомендується для випадків коли Re <105)
б) 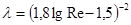 - формула Конакова (рекомендується для випадків коли Re > 105). Також рекомендуються і інші формули.
- формула Конакова (рекомендується для випадків коли Re > 105). Також рекомендуються і інші формули.
Для гідравлічно гладких труб втрати напору за довжиною залежить від швидкості в степені 1,75 ( ).
).
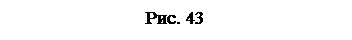
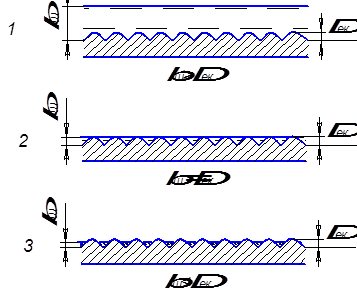 Друга зона – перехідна зона гідравлічних опорів. В цій зоні
Друга зона – перехідна зона гідравлічних опорів. В цій зоні  . (рис.43. 2). тобто, при збільшені швидкості руху рідини в трубі пристінний шар зменшується до такої величини (згідно формули
. (рис.43. 2). тобто, при збільшені швидкості руху рідини в трубі пристінний шар зменшується до такої величини (згідно формули  ), що торкається виступів шорсткості, при цьому симплекс
), що торкається виступів шорсткості, при цьому симплекс  . В цій зоні
. В цій зоні  коефіцієнт опору тертя залежить не тільки від Re, але і від відносної шорсткості
коефіцієнт опору тертя залежить не тільки від Re, але і від відносної шорсткості 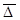 , так як рідина в пристінному шарі між виступами шорсткості ще рухається в ламінарному режимі і в цей же час ядро турбулентного потоку чіпляється за виступи шорсткості, при цьому виникають часткові збурення, що впливає на величину
, так як рідина в пристінному шарі між виступами шорсткості ще рухається в ламінарному режимі і в цей же час ядро турбулентного потоку чіпляється за виступи шорсткості, при цьому виникають часткові збурення, що впливає на величину 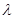 (
(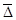 відносна шорсткість, яка дорівнює відношенню абсолютної шорсткості до діаметра труби, тобто
відносна шорсткість, яка дорівнює відношенню абсолютної шорсткості до діаметра труби, тобто 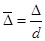 ).
).
Для визначення 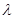 в перехідній зоні рекомендується формула Альтшуля
в перехідній зоні рекомендується формула Альтшуля
 .
.
В цій зоні втрати напору за довжиною залежить від швидкості в степені від 1,75 до 2,0 (1.85). і її прийнято називати доквадратичною зоною гідравлічних опорів.
третя зона гідравлічних опорів відповідає випадку коли 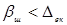 і називається зоною гідравлічно шорстких труб. Тут збільшення швидкості рідини (в порівнянні з доквадратичною зоною) приводить до зменшення величини
і називається зоною гідравлічно шорстких труб. Тут збільшення швидкості рідини (в порівнянні з доквадратичною зоною) приводить до зменшення величини  , при якій пристінний шар знаходиться між виступами шорсткості і ця величина значно менша за
, при якій пристінний шар знаходиться між виступами шорсткості і ця величина значно менша за 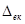 (рис. 43. 3). тобто, в цій зоні
(рис. 43. 3). тобто, в цій зоні 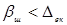 і з іншого боку
і з іншого боку 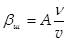 . тоді, сиплекс
. тоді, сиплекс
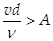 .
.
дослідами встановлено, що для зони гідравлічно-шорстких труб А >1260.
Таким чином при  внутрішня поверхня труби називається гідравлічно-шорсткою. При цьому
внутрішня поверхня труби називається гідравлічно-шорсткою. При цьому 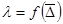 і не залежить від Re. В цій зоні втрати напору за довжиною залежать від швидкості в другій степені (
і не залежить від Re. В цій зоні втрати напору за довжиною залежать від швидкості в другій степені ( ). Тому зона гідравлічно шорстких труб називається квадратичною зоною гідравлічних опорів.
). Тому зона гідравлічно шорстких труб називається квадратичною зоною гідравлічних опорів.
Оскільки в зоні гідравлічно-шорстких труб число Re має велике значення, то в формулі Альтшуля (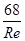 ) значно менше ніж (
) значно менше ніж (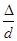 ) і величиною (
) і величиною (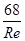 ) можна знехтувати. Тоді розрахункова формула для третьої зони буде
) можна знехтувати. Тоді розрахункова формула для третьої зони буде  (формула Шифринсона). Також для цієї зони гідравлічних опорів є формули інших авторів для визначення
(формула Шифринсона). Також для цієї зони гідравлічних опорів є формули інших авторів для визначення 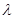 .
.
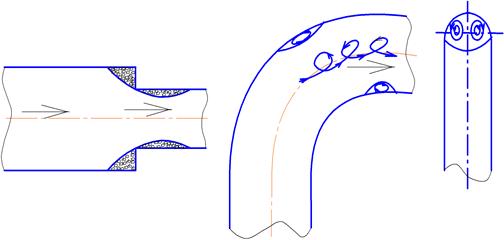
Наведений матеріал стосується течії рідин в трубах круглого перерізу, яка найчастіше зустрічається на практиці. Але на хлібокомбінатах, елеваторах у вентиляційних системах, в сантехніці застосовують, крім труб круглого перерізу інші форми перерізів (квадратні, прямокутні; в нагрівальних приладах – еліптичні перерізи і т.ін.) (рис. 44).
Для визначення в трубах некруглого перерізу числа Re і hl замість d діаметра труби приймається гідравлічний радіус R. при цьому числа Re і їх критичні значення будуть іншими.
Для гідравлічного розрахунку трубопроводів некруглого перерізу застосовують поняття еквівалентного діаметра, який дорівнює
 . (117)
. (117)
За допомогою величини dекв визначають втрати напору за формулою Дарсі-Вейсбаха, а також інші характеристики руху як і для круглих труб. Тобто, трубопровід довільної форми замінюють круглою, якому властивий такий самий гідравлічний опір, місцеві опори і втрати напору. 
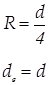




 Місцеві втрати напору в трубопроводах і каналах виникають в місцях перешкод на шляху руху рідини. До місцевих опорів належить: запірна арматура (вентилі, засувки, крани, клапани), фасонні частини трубопроводів (коліна, раптові і поступові, розширення і звуження, трійники, хрестовини та ін.), сітки, фільтри і багато інших пристроїв.
Місцеві втрати напору в трубопроводах і каналах виникають в місцях перешкод на шляху руху рідини. До місцевих опорів належить: запірна арматура (вентилі, засувки, крани, клапани), фасонні частини трубопроводів (коліна, раптові і поступові, розширення і звуження, трійники, хрестовини та ін.), сітки, фільтри і багато інших пристроїв.
Утворення вихрових зон і поява в деяких конструкціях місцевих опорів вторинних течій, різка зміна конфігурацій живих перерізів зі зміною швидкостей в конкретних конструкціях приводять до виникнення втрат напору (рис. 45).
При ламінарному русі рідини вихрові зони не виникають. У цьому випадку місцеві опори є наслідком значних змін швидкості, що утворюються геометрією місцевої перешкоди рухові.
В основному режим руху рідини в місцевих перешкодах – турбулентний і відповідає квадратичної зони гідравлічних опорів.
Кожна конструкція (тип) місцевого опору характеризується коефіцієнтом місцевого опору 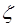 .
.
Втрати напору при проходженні рідини через місцевий опір визначається за формулою
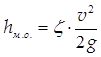 , (118)
, (118)
де 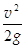 – швидкісний напір за місцевим опором.
– швидкісний напір за місцевим опором.
Дослідами встановлено, що величини коефіцієнтів місцевих опорів при ламінарному режимі і перехідному режимах руху залежать від Re. Загальний вигляд цієї залежності
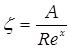 , (119)
, (119)
де А і x - коефіцієнт, що залежить від виду місцевого опору і умов руху рідини.
При турбулентному русі рідини коефіцієнт 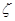 не залежить від Re і є характеристикою даного місцевого опору.
не залежить від Re і є характеристикою даного місцевого опору.
В абсолютній більшості коефіцієнти місцевих опорів визначаються дослідним шляхом (крім коефіцієнта місцевого опору при раптовому розширенні потоку). У довідниках значення 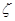 даються для квадратичної зони турбулентного режиму, тобто вони сталі для даного виду місцевого опору.
даються для квадратичної зони турбулентного режиму, тобто вони сталі для даного виду місцевого опору.
В промисловій практиці рідини рухаються в більшості випадків турбулентно, тому втрати напору (енергії) в трубопроводах сталого діаметру з значною кількістю місцевих опорів визначаються залежністю
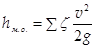 , (120)
, (120)
де 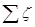 – сума коефіцієнтів місцевих опорів,
– сума коефіцієнтів місцевих опорів,
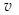 – швидкість рідини в трубі сталого діаметру.
– швидкість рідини в трубі сталого діаметру.
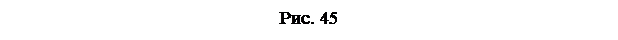 Eквівалентна довжина трубопроводу це така його довжина, на якій втрати напору hlекв будуть дорівнювати втратам напору на даному місцевому опорі.
Eквівалентна довжина трубопроводу це така його довжина, на якій втрати напору hlекв будуть дорівнювати втратам напору на даному місцевому опорі.
Тобто 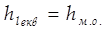 , або
, або
 ,
,
звідки  , м. (120)
, м. (120)
У довідниках приводяться еквівалентні довжини трубопроводів, які відповідають певним місцевим опорам. Значення коефіцієнтів місцевих опорів відносяться до стабілізованих (вирівняних) потоків. Але у коротких трубопроводах, де місцеві опори розташовані близько один від одного, потік надходить до наступного опору не досить вирівнюваним, внаслідок чого втрати у цих опорах, а також їх сума будуть іншими, ніж при розташовані цих самих опорів на великій відстані один від одного. (Дані про взаємний вплив місцевих опорів теж наводиться у довідника)
 2017-10-25
2017-10-25 671
671








