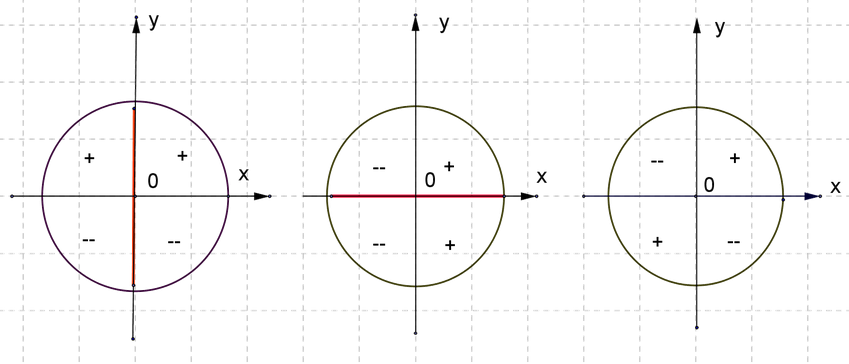
Sin x cos x tg x ctg x
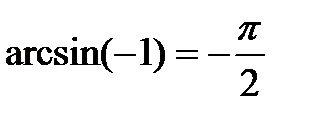
| 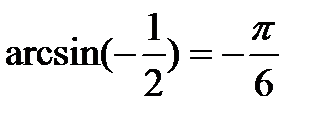
| 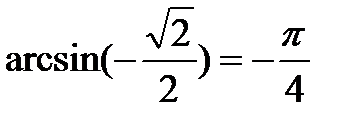
| 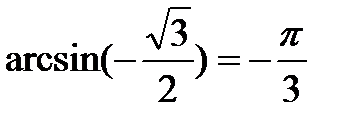
|
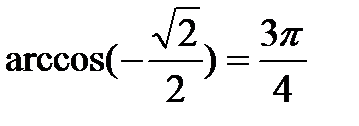
| 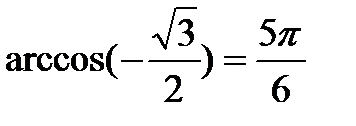
| 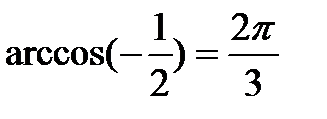
| 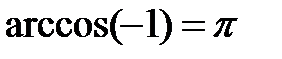
|
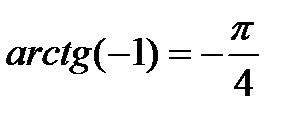
| 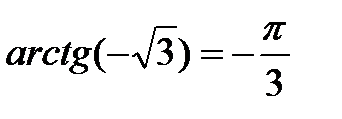
| 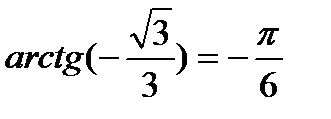
| 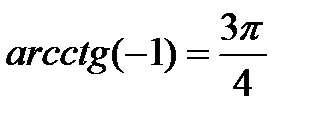
|
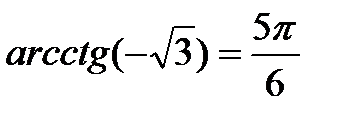
| 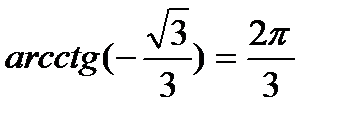
|
Простейшие тригонометрические уравнения и частные случаи
sin t = a, 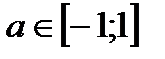 t = (-1) n arcsin a + πn, n
t = (-1) n arcsin a + πn, n 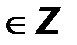 Частные случаи:
sin t = 1
Частные случаи:
sin t = 1 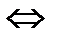 t = t = 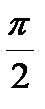 + 2πn, n + 2πn, n 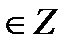 sin t = - 1
sin t = - 1 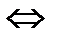 t = - t = - 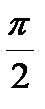 + 2πn, n + 2πn, n 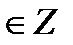 sin t = 0
sin t = 0 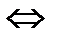 t = πn, n t = πn, n 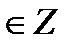
| cos t = a,  t = ± arccos a + 2πn, n
t = ± arccos a + 2πn, n 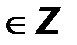 Частные случаи:
сos t = - 1
Частные случаи:
сos t = - 1 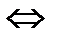 t = π + 2πn, n t = π + 2πn, n 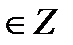 cos t = 0
cos t = 0 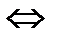 t = t = 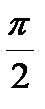 + πn, n + πn, n 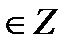 cos t = 1
cos t = 1 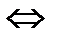 t = 2πn, n t = 2πn, n 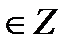
|
tg t = a
t = arctg a + πn, n 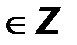 Частные случаи:
tg t = 1
Частные случаи:
tg t = 1 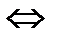 t = t = 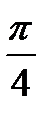 + πn, n + πn, n 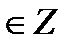 tg t = - 1
tg t = - 1 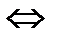 t = - t = - 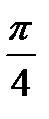 + πn, n + πn, n 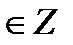 tg t = 0
tg t = 0 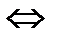 t = πn, n t = πn, n 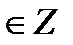
| ctg t = a
t = arcctg a + πn, n 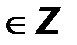 Частные случаи:
ctg t = 1
Частные случаи:
ctg t = 1 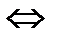 t = t = 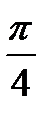 + πn, n + πn, n 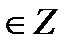 ctg t = - 1
ctg t = - 1 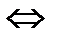 t = t = 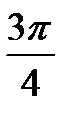 + πn, n + πn, n 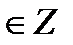 ctg t = 0
ctg t = 0 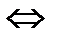 t = t = 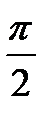 πn, n πn, n 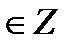
|
Формулы сложения аргументов
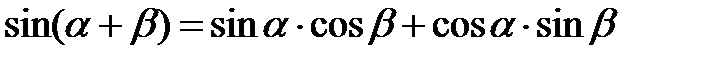
| 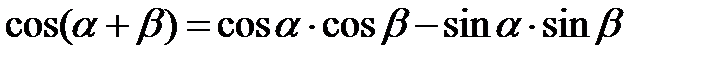
|
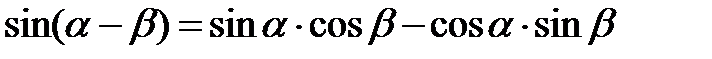
| 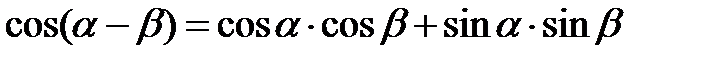
|
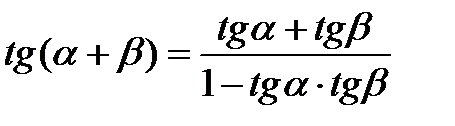 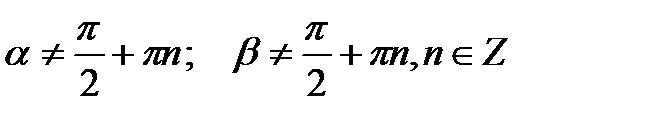
| 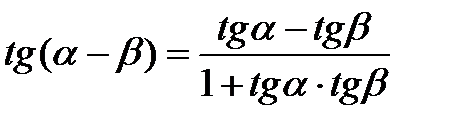 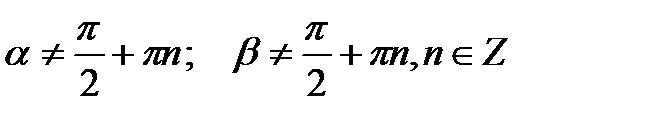
|
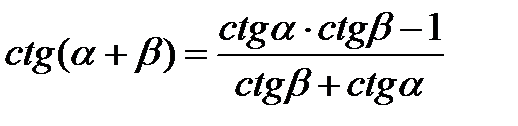 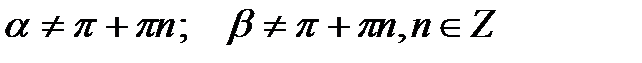
| 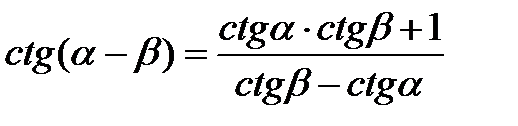 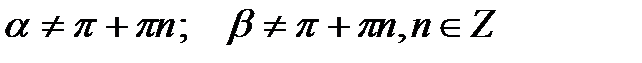
|
Формулы двойного угла
sin2α = 2sinα  cosα cosα
| cos2α = cos2 α – sin2 α |
| cos2α = 2cos2 α – 1 = 1 – 2sin2 α | |
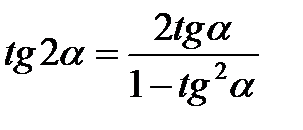
| 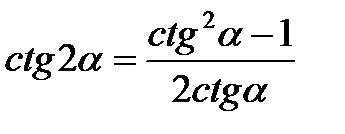
|
Формулы сложения одноимённых функций
sinα+sinβ = 2sin 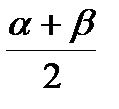 cos cos 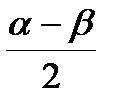
| cosα+cosβ= 2cos 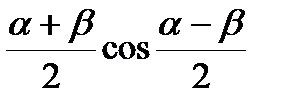
|
sinα – sinβ = 2sin 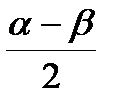 cos cos 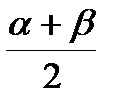
| cosα–cosβ=-2sin 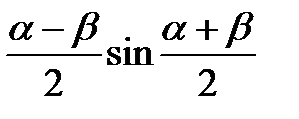
|
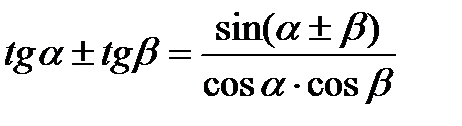
| 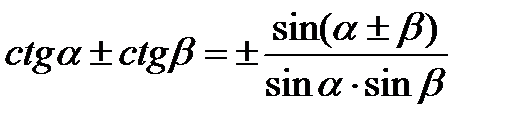
|
Формулы половинного угла
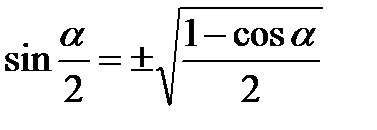
| 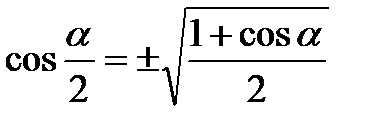
| |
sinα = 2sin 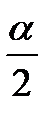 cos cos 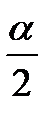
| cosα = cos2 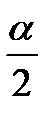 – sin2 – sin2 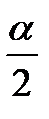
| |
cosα =2cos2 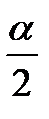 – 1 = 1 – 2sin2 – 1 = 1 – 2sin2 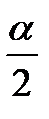
| ||
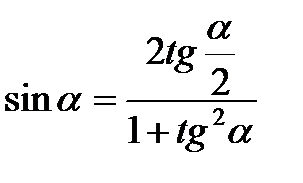
| 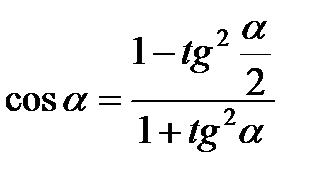
| |
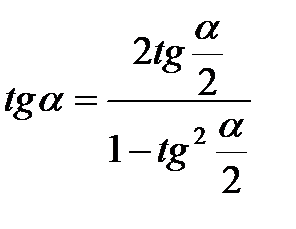
| 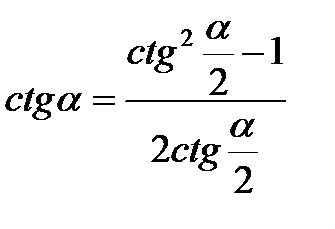
| |
Преобразование произведения тригонометрических функций в алгебраическую сумму
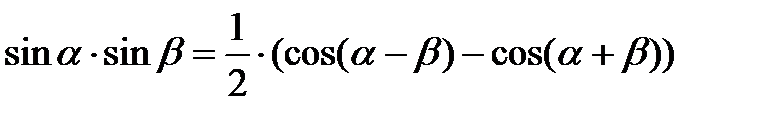
| 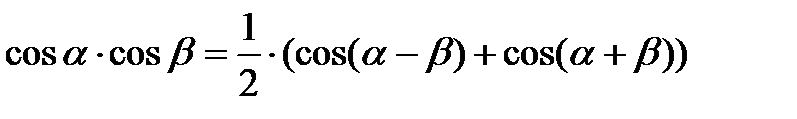
|
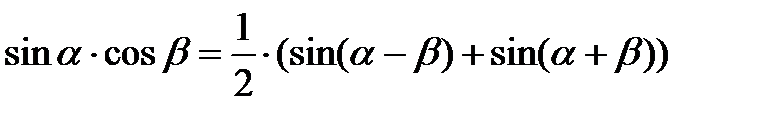
|
Производная. Применение производной
Таблица производных
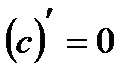
| 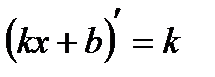
| |
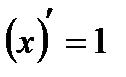
| 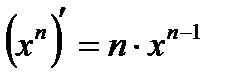
| |
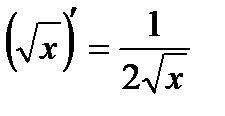
| 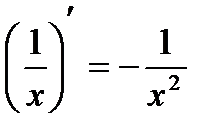
| |
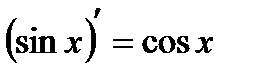
| 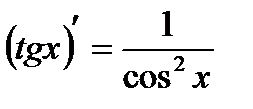
| |
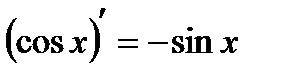
| 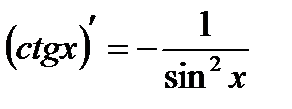
| |
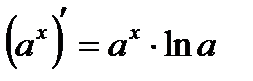
| 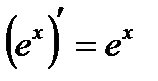
| |
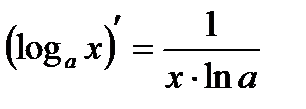
| 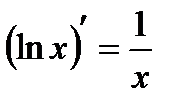
| |
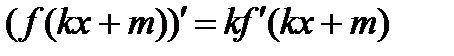 (производная сложной функции)
(производная сложной функции)
| ||
| Правила дифференцирования | ||
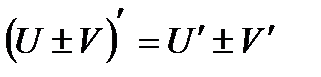
| 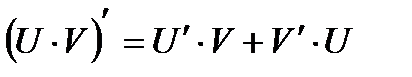
| |
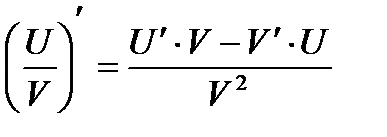
| 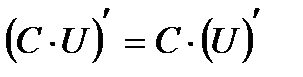
| |
Алгоритм составления уравнения касательной
к графику функции у = f(х) в точке х = а.
- Обозначим абсциссу точки касания буквой а.
- Вычислим f(a).
- Найдем f '(х) и вычислим f '(а).
- Подставим значения числа а, f(а), f '(а) в уравнение касательной.
5. Записать получившееся уравнение y = f(a) + f '(а) · (x-a) и привести к виду у = kx+b.
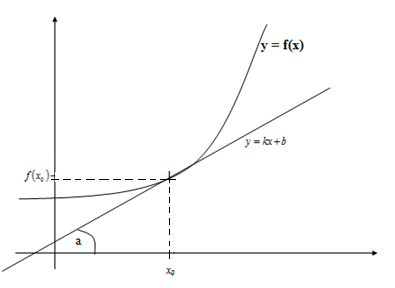
Геометрический смысл производной функции у = f(х).
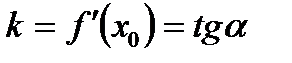 (
(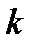 - угловой коэффициент)
- угловой коэффициент)
 2017-11-01
2017-11-01 535
535








