Пусть  ,
, 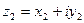 или в тригонометрической форме
или в тригонометрической форме  ,
,
Сложение и вычитание
 .
.
Умножение
 . С учетом того, что
. С учетом того, что  , получим окончательное выражение для произведения:
, получим окончательное выражение для произведения:
 .
.
Получим формулу для произведения двух комплексных чисел в тригонометрической форме:

т.е.
 .
.
В случае комплексно-сопряженных чисел

Деление
 , откуда
, откуда
 .
.
В тригонометрической форме:  .
.
Возведение в степень
С учетом формулы для произведения комплексных чисел в тригонометрической форме
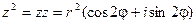 . В общем случае справедлива следующая формула:
. В общем случае справедлива следующая формула:
 ,
,
где 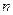 - целое положительное число. Это выражение называется формулой Муавра.
- целое положительное число. Это выражение называется формулой Муавра.
Извлечение корня

Возводя в n-ю степень, получим:

Отсюда: 
 .
.
В итоге получим: 
Если  , то
, то  ,
,  , то
, то  , …
, …  , то
, то  ,
,  , то
, то  ,
, 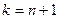 , то
, то  , …
, …
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений при  . При
. При  значения корня начинают повторяться.
значения корня начинают повторяться.
Пример
Пусть  ;
;  . Найти:
. Найти:  ,
, 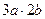 ,
,  ,
,  ,
,  .
.
Решение
1)  .
.
2)  .
.
3)  .
.
4)  .
.
5)  .
.
6) Общая формула для корня 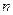 -ой степени из комплексного числа
-ой степени из комплексного числа  :
:
 .
.
В нашем случае  , тогда
, тогда  (поскольку извлекается корень 3-ей степени),
(поскольку извлекается корень 3-ей степени),  ,
,  , откуда
, откуда  . Как было сказано выше, корень n – ой степени из комплексного числа имеет n различных значений при
. Как было сказано выше, корень n – ой степени из комплексного числа имеет n различных значений при  , то есть в нашем случае – три различных значения при
, то есть в нашем случае – три различных значения при  . Тогда:
. Тогда:
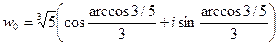 ;
;
 ;
;
 .
.
 2017-11-01
2017-11-01 474
474







