2017-11-01
1609
Комплексные числа
Определение Комплексным числом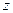 
называется выражение 
, где 
и 
– действительные числа,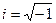 
– мнимая единица. При этом называется действительной частью числ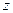а (
), а - мнимой частью числа (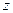
).
Если 
, то число 
будет чисто мнимым, если 
, то число 
будет действительным.
Определение Числа и 
называются комплексно-сопряженными.
Определение Два комплексных числа 
и 
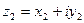называются равными, если соответственно равны их действительные и мнимые части: 
.
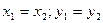Определение Комплексное число равно нулю, если равны нулю его действительная и мнимая части: 
Понятие комплексного числа имеет геометрическую интерпретацию. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью. Таким образом, на оси 
располагаются действительные числа, а на оси 
– чисто мнимые.
Полярная система координат
Полярная система координат на плоскости задается точкой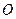 
, которая называется полюсом, и лучом, который называется полярной осью. Координатами точки в полярной системе координат являются расстояние точки от полюса 
и угол 
между полярной осью и радиус-вектором этой точки. Этот угол называется полярным углом.
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси :
Из геометрических соображений видно, что координаты точки 
в декартовой и полярной системах координат связываются соотношениями: 
; 
; 
; 
. Тогда комплексное число 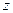можно переписать в виде: 
.
Такая форма записи называется тригонометрической формой записи комплексного числа. При этом величина называется модулем комплексного числа, а угол наклона - аргументом комплексного числа.
Очевидно, что комплексно-сопряженные числа имеют одинаковые модули и противоположные аргументы.
