Однофазная электрическая цепь – это цепь переменного тока, состоящая из приёмников электрической энергии, получающих питание от однофазного генератора синусоидальной ЭДС.
В качестве приемников электрической энергия в цепь переменного тока могут быть включены резистивный элемент (активное сопротивление  ) и реактивные элементы: катушка индуктивности и конденсатор, характеризуемые соответственно параметрами L и С.
) и реактивные элементы: катушка индуктивности и конденсатор, характеризуемые соответственно параметрами L и С.
Возможны две схемы включения этих приемников:
1) последовательное соединение активного сопротивления r, индуктивности L и емкости С (рис. 1);
2) параллельное соединение активного сопротивления 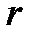 , индуктивности L и емкости С (рис. 2).
, индуктивности L и емкости С (рис. 2).
В цепи последовательного соединения 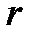 , L, C (рис. 1) все приемники характеризуются одним и тем же синусоидальным током
, L, C (рис. 1) все приемники характеризуются одним и тем же синусоидальным током  ,
,
который протекает под действием синусоидального напряжения, приложенного к цепи
где  – соответственно мгновенные значения тока и напряжения;
– соответственно мгновенные значения тока и напряжения;
 – cответственно амплитудные значения тока и напряжения;
– cответственно амплитудные значения тока и напряжения;
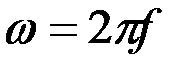 – угловая частота (
– угловая частота ( – частота);
– частота);  – время;
– время;
φ - сдвиг фаз между напряжением и током.
Измерительные приборы (амперметр, вольтметр) регистрируют так называемые действующие значения переменного тока  и напряжения
и напряжения  :
:
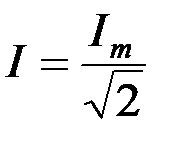 ,
,  .
.
Расчеты электрических цепей, как правило, ведутся для действующих значений тока и напряжения.
Ток в цепи последовательного соединения 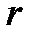 , L, C (см. рис. 1) создает на каждом из участков этой цепи падения напряжения, равные произведению тока на сопротивление участка. Напряжение на активном сопротивлении
, L, C (см. рис. 1) создает на каждом из участков этой цепи падения напряжения, равные произведению тока на сопротивление участка. Напряжение на активном сопротивлении  совпадает по фазе с током (рис. 3). Напряжение на индуктивности
совпадает по фазе с током (рис. 3). Напряжение на индуктивности  опережает по фазе ток на угол
опережает по фазе ток на угол  , причем коэффициент пропорциональности между индуктивным напряжением и током
, причем коэффициент пропорциональности между индуктивным напряжением и током  называется индуктивным сопротивлением. Напряжение на емкости
называется индуктивным сопротивлением. Напряжение на емкости 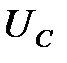 отстает по фазе от тока на угол
отстает по фазе от тока на угол  и равно
и равно  , где
, где  – емкостное сопротивление.
– емкостное сопротивление.
Вектор действующего значения напряжения на входных зажимах согласно второму закону Кирхгофа равен геометрической сумме действующих значений напряжений на отдельных участках цепи т.е.
 | (1) |
Поэтому на векторной диаграмме напряжений и токов (рис.3), представляющей собой графическое решение уравнения (1), вектор полного напряжения  замыкает многоугольник векторов
замыкает многоугольник векторов  ,
,  ,
,  . Диаграмма напряжений построена для случая, когда
. Диаграмма напряжений построена для случая, когда  . Как видно из диаграммы напряжений,
. Как видно из диаграммы напряжений,
 | (2) |
 , (2)
, (2)
где  – реактивное напряжение;
– реактивное напряжение;  .
. 
На векторной диаграмме (рис. 3) треугольник OAB называется треугольником напряжений.
Подставляя в формулу (2) значения напряжений 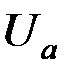 ,
, 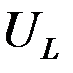 ,
,  , получим
, получим
 ,
,
откуда
 | (3) |
Выражение (3) представляет собой закон Ома для последовательной цепи переменного тока, причем  – полное сопротивление цепи;
– полное сопротивление цепи;
 ,
,
где  – реактивное сопротивление цепи;
– реактивное сопротивление цепи;  .
.
Разделив стороны треугольника напряжений (рис. 3) на ток  , получим подобный треугольник сопротивлений (треугольник OM1N1 (рис. 4)).
, получим подобный треугольник сопротивлений (треугольник OM1N1 (рис. 4)).
В цепи с параллельным соединением 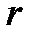 , L, C (см. рис. 2) все приемники находятся под одним и тем же напряжением питающей сети
, L, C (см. рис. 2) все приемники находятся под одним и тем же напряжением питающей сети  . Согласно первому закону Кирхгофа для действующих значений, вектор тока
. Согласно первому закону Кирхгофа для действующих значений, вектор тока  в неразветвлённой части цепи равен геометрической сумме токов параллельных ветвей:
в неразветвлённой части цепи равен геометрической сумме токов параллельных ветвей:
 | (4) |
По уравнению (4) на рис. 4,а построена векторная диаграмма токов. Активный ток  совпадает по фазе с напряжением и определяется по формуле
совпадает по фазе с напряжением и определяется по формуле  , где
, где  – активная проводимость.
– активная проводимость.
Индуктивный ток  отстает по фазе от напряжения на угол
отстает по фазе от напряжения на угол 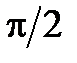 ;
;  , где
, где  – индуктивная проводимость.
– индуктивная проводимость.
Емкостной ток  опережает по фазе напряжение на угол
опережает по фазе напряжение на угол 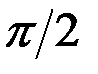 ;
;  , где
, где  – ёмкостная проводимость.
– ёмкостная проводимость.
Как видно из диаграммы токов (рис. 5), полный ток
 ,
,
где  – реактивный ток;
– реактивный ток; 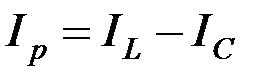 .
.
Векторную диаграмму токов (рис. 5) называют треугольником токов (треугольник ОAB). Разделив стороны треугольника токов на напряжение U, подучим треугольник проводимостей OAB, сторонами которого будут:  – активная проводимость;
– активная проводимость;  – реактивная проводимость;
– реактивная проводимость;  – полная проводимость.
– полная проводимость.
 ) и реактивные элементы: катушка индуктивности и конденсатор, характеризуемые соответственно параметрами L и С.
) и реактивные элементы: катушка индуктивности и конденсатор, характеризуемые соответственно параметрами L и С.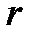 , индуктивности L и емкости С (рис. 2).
, индуктивности L и емкости С (рис. 2).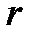 , L, C (рис. 1) все приемники характеризуются одним и тем же синусоидальным током
, L, C (рис. 1) все приемники характеризуются одним и тем же синусоидальным током  ,
,
 – соответственно мгновенные значения тока и напряжения;
– соответственно мгновенные значения тока и напряжения; – cответственно амплитудные значения тока и напряжения;
– cответственно амплитудные значения тока и напряжения;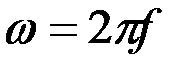 – угловая частота (
– угловая частота ( – частота);
– частота);  – время;
– время; и напряжения
и напряжения  :
: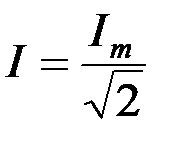 ,
,  .
.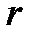 , L, C (см. рис. 1) создает на каждом из участков этой цепи падения напряжения, равные произведению тока на сопротивление участка. Напряжение на активном сопротивлении
, L, C (см. рис. 1) создает на каждом из участков этой цепи падения напряжения, равные произведению тока на сопротивление участка. Напряжение на активном сопротивлении  совпадает по фазе с током (рис. 3). Напряжение на индуктивности
совпадает по фазе с током (рис. 3). Напряжение на индуктивности  опережает по фазе ток на угол
опережает по фазе ток на угол  , причем коэффициент пропорциональности между индуктивным напряжением и током
, причем коэффициент пропорциональности между индуктивным напряжением и током  называется индуктивным сопротивлением. Напряжение на емкости
называется индуктивным сопротивлением. Напряжение на емкости 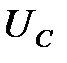 отстает по фазе от тока на угол
отстает по фазе от тока на угол  и равно
и равно  , где
, где  – емкостное сопротивление.
– емкостное сопротивление.
 замыкает многоугольник векторов
замыкает многоугольник векторов  ,
,  ,
,  . Диаграмма напряжений построена для случая, когда
. Диаграмма напряжений построена для случая, когда  . Как видно из диаграммы напряжений,
. Как видно из диаграммы напряжений,
 , (2)
, (2) – реактивное напряжение;
– реактивное напряжение;  .
. 
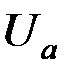 ,
, 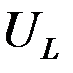 ,
,  , получим
, получим ,
,
 – полное сопротивление цепи;
– полное сопротивление цепи; ,
, – реактивное сопротивление цепи;
– реактивное сопротивление цепи;  .
. , получим подобный треугольник сопротивлений (треугольник OM1N1 (рис. 4)).
, получим подобный треугольник сопротивлений (треугольник OM1N1 (рис. 4)).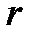 , L, C (см. рис. 2) все приемники находятся под одним и тем же напряжением питающей сети
, L, C (см. рис. 2) все приемники находятся под одним и тем же напряжением питающей сети  . Согласно первому закону Кирхгофа для действующих значений, вектор тока
. Согласно первому закону Кирхгофа для действующих значений, вектор тока  в неразветвлённой части цепи равен геометрической сумме токов параллельных ветвей:
в неразветвлённой части цепи равен геометрической сумме токов параллельных ветвей:
 совпадает по фазе с напряжением и определяется по формуле
совпадает по фазе с напряжением и определяется по формуле  , где
, где  – активная проводимость.
– активная проводимость. отстает по фазе от напряжения на угол
отстает по фазе от напряжения на угол 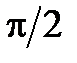 ;
;  , где
, где  – индуктивная проводимость.
– индуктивная проводимость. опережает по фазе напряжение на угол
опережает по фазе напряжение на угол 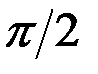 ;
;  , где
, где  – ёмкостная проводимость.
– ёмкостная проводимость. ,
, – реактивный ток;
– реактивный ток; 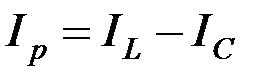 .
. – активная проводимость;
– активная проводимость;  – реактивная проводимость;
– реактивная проводимость;  – полная проводимость.
– полная проводимость. 2017-11-01
2017-11-01 720
720







