Цепи однофазного переменного тока (ОПТ)

Элементы цепи ОПТ и их свойства

Однофазным переменным током называют ток, меняющийся по закону синуса / косинуса:

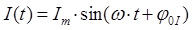
Здесь I_m - амплитуда колебаний тока; ω=2πν - циклическая частота колебаний; φ_0I - начальная фаза колебаний.

Источниками переменного тока являются генераторы переменного тока, чье напряжение меняется по аналогичному закону. Цепи переменного тока формируются так же, как и цепи постоянного тока, т.е содержат источник электрической энергии и потребителей этой энергии. Эти цепи могут быть простыми и сложными, разветвленными и неразветвленными, с одним или несколькими источниками напряжения. Для токов и напряжений в таких цепях также справедливы первый и второй законы Кирхгофа, законы Ома, Джоуля-Ленца и т.д.

Однако физические процессы в таких цепях намного сложнее и разнообразнее, чем в цепях постоянного тока. Здесь уместна их аналогия с фото и видео: хотя любое видео, технологически, сводится к большой совокупности фотографий, его информационные возможности несопоставимо богаче информационных возможностей фотографий.

Соответственно, математическое описание переменного тока требует более сложного математического аппарата и графического инструментария.

Основными элементами цепи переменного тока являются:

1) источники переменного напряжения, E (U)

2) резисторы, R

3) конденсаторы (емкости), С

4) катушки (индуктивности), L

Первые два типа элементов присутствуют и в цепях постоянного тока. Однако два последних в них не используются: 1) конденсаторы создают разрывы в цепи и не пропускают постоянный ток; 2) катушки пропускают постоянный ток, но обладают в нем нулевым сопротивлением, и, следовательно, не оказывают на распределение токов и напряжений никакого влияния.

Если конденсатор включить в цепь с переменным напряжением, то амперметр зарегистрирует наличие тока. Это значит, что он пропускает переменный ток. Как такое возможно? Причина заключается в том, что разрыв, создаваемый конденсатором в цепи, не является препятствием для электрического поля, через которое заряды на одной пластине конденсатора влияют на заряды другой. При постоянном токе это взаимодействие прекращает ток - заряды, набежавшие на пластину ближайшую к источнику тока, останавливают набегающие от источника заряды путем их отталкивания.

В переменном токе это взаимодействие, наоборот, поддерживает ток, приводя в движение заряды по другую сторону разрыва. Что касается взаимодействия набежавших и набегающих зарядов на пластине, обращенной к источнику тока, то оно вызывает не прекращение тока, а лишь его торможение. В результате конденсатор оказывает сопротивление току и создает на себе падение напряжения.

Если, аналогично, включить в цепь переменного тока катушку, то вольтметр зарегистрирует на ней падение напряжения, что является признаком появления у ней сопротивления. Откуда оно взялось - ведь в постоянном токе катушка обладает нулевым сопротивлением?

Ответ кроется в явлении электромагнитной индукции (ЭМИ). При изменении тока в катушке, изменяется ее магнитное поле, а согласно закону ЭМИ изменение последнего порождает вихревое электрическое поле. Согласно правилу Ленца вихревое поле ЭМИ всегда противофазно полю создающему ток и, следовательно, оказывает ему сопротивление.

Появление в цепях переменного тока катушек и конденсаторов кардинально меняет их (цепей) электрические свойства.

Это проявляется в:

1) расфазировке (рассогласовании) колебаний тока и напряжения;

2) реактивном характере потребления энергии

Первое свойство означает несовпадение динамики изменения тока и напряжения как на конденсаторе, так и на катушке, а именно: когда напряжение по модулю максимально, ток равен нулю, и наоборот. Второе свойство означает принципиально новую форму потребления энергии - и катушка и конденсатор, забирая энергию у источника тока, возвращают ее затем ему обратно.

Реактивностью, реакцией, как известно, называют свойство объекта формировать отклик (реакцию) на внешнее воздействие. Например реактивное движение возникает как результат ответного влияния отбрасываемого объекта на отбрасывающий объект (ракета, морские моллюски и т.д.). Реактивный характер потребления энергии выражается в последующем отбрасывании от себя полученной энергии.

Расфазировка колебаний тока и напряжения на конденсаторе определяется противоположным характером влияния накопленного им заряда на ток и напряжение:

1) чем больше заряда оказывается на конденсаторе, тем меньше к нему ток, так как набежавшие заряды отталкивают набегающие;

2) чем больше заряда на конденсаторе, тем силнее его электрическое поле, - и тем больше напряжение

Расфазировка колебаний тока и напряжения на катушке определяется противоречивым характером влияния тока на величину вихревого поля ЭМИ:

а) наибольшую ЭДС ЭМИ ток создает при нулевом значении (в этот момент он, - а следовательно и магнитное поле, - изменяется быстрее всего);

б) наименьшую ЭДС ЭМИ (ноль) ток создает при максимальном значении, когда его рост прекращается.

Наиболее наглядно точный характер расфазировки колебаний тока и напряжения можно показать на временных диаграммах (рис.6, рис.7) Сплошными линиями на графиках показаны синусоиды колебания напряжения, пунктирными - тока.

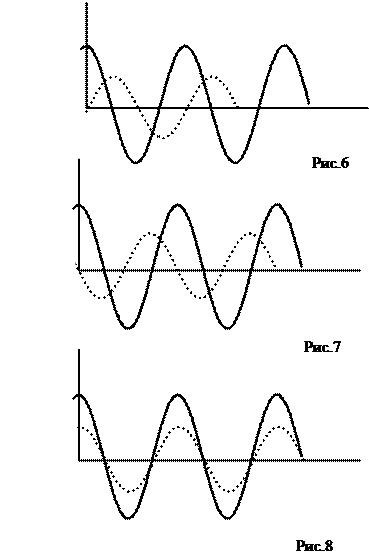
Рисунок 6 показывает как соотносятся колебания этих параметров на катушке, а рисунок 7 - на конденсаторе. Сдвиг в фазах в обоих случаях одинаков и составляет 90⁰, однако при одной и той же фазе напряжения, фазы токов в катушке и конденсаторе противоположны. Говорят, что напряжение в катушке опережает ток на 90⁰, а на конденсаторе - отстает. Это следует из того, что ток на катушке идет в область положительных значений, с некоторым запаздыванием по отношению к напряжению, а у конденсатора - с опережением.

Физически это объяснимо:

1) в катушке при большом внешнем напряжениивозникает противоположная по знаку эдс ЭМИ - в результате ток в ней подавляется; он начинает нарастать лишь по мере ее ослабевания;

2) в конденсаторе, наоборот - даже при нулевом значении напряжения ток уже достигает максимальной величины, что есстественно: отсутствие напряжения означает отсутствие на конденсаторе зарядов и, как следствие, – отсутствие какого-либо сопротивления набегающим зарядам.

Наконец на рисунке 8 показаны ко-лебания тока и напряжения на резисторе. Здесь никакой расфазировки не наблюдается, так как падение напряжения создается самим током (а не зарядами или ЭДС, как у конденсатора или катушки).

Векторные диаграммы цепей ОПТ

Рассогласование колебаний тока и напряжения на реактивных элементах ОПТ (т.е. катушке и конденсаторе) резко усложняет их математическое и даже наглядное описание. Действительно, если электрическая цепь состоит из большого количества таких разнородных элементов, то, например, при втекании в один провод пяти расфазированных токов, суммарный ток будет представлять «кашу» из синусоид и определение суммарного тока может оказаться весьма сложной задачей (ситуация оказывается похожей на описание поведения поверхности воды под дождем).

Для решения этой проблемы используется метод векторных диаграмм (ВД). На них колебания каждого электрического параметра ассоциируют с вращающимся вектором (например, вращающийся на нити шарик создает на стене, - при его освещении, - колеблющуюся тень). Если в один провод втекает несколько токов, то на ВД для такого провода рисуют соответствующее количество векторов. Так как все токи колеблются, то соответствующие им вектора на ВД должны находиться в совместном вращении. Однако важнейшей особенностью колебаний любых электрических параметров в цепях ОПТ является одинаковость их периодов.

На ВД это выражается в одинаковой скорости вращения всех векторов. Последнее означает неподвижность этих вектров относительно друг друга, а следовательно непринципиальность самого факта вращения. Это позволяет изобразить все колеблющиеся электрические параметры в виде неподвижных векторов.

Наличие вращения, тем не менее, учитывают через:

1) увязывание угла, под которым рисуется вектор на графике, с циклической частотой и фазой колебания всех электрических параметров φ = ω?t + φ₀ =2πν?t + φ₀;

2) выбором положительного отсчета углов и направления вращения векторов (теперь уже «воображаемого») против часовой стрелки.

Если требуется учесть колебания всех электрических параметров цепи, то независимо от того на каких участках полной цепи они появляются, все их можно отобразить на одно й диаграмме, поскольку принципиальное значение имеет лишь временная расфазировка

Пространственная расфазировка в цепях ОПТ отсутствует из-за огромной скорости распрос-транения электромагнитных взаимодействий, т.е. в любой точке цепи в заданны й момент времени все значения рассматриваемого параме-тра имеют одну и туже фазу колебания.

Предположим, что втекающие в один провод несколько токовмы изобразили в виде нескольких векторов а, b, c (рис.9). Каким образом можно найти полный ток? Ответ на этот вопрос теперь уже не представляет сложности - для этого используем правило векторного сложения, которое имеет несколько вариантов применения:

1) в виде известного правила «параллелограма»;

2) в виде правила последовательного соединения складываемых векторов друг за другом (начало последующего вектора соединяем с концом предыдущего - итоговый вектор соединяет начало самого первого вектора с концом самого последнего (рис.9).

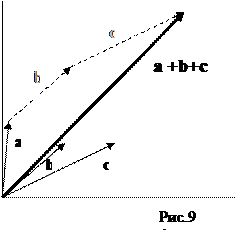
Если все сказанное применить теперь к векторному способу отображения колебаний тока и напряжения на катушке, конденсаторе и резисторе, то получим ВД на рис.10, рис.11, рис.12. (длинный вектор соответствует напряжению, короткий - току). На рис. 10 видно, что в катушке значениям тока и напряжения, отмеченным черными кружками на временнóй диаграмме, соответствует положения векторов на левой круговой диаграмме; правая круговая диаграмма иллюстрирует точную ориентацию и угол между векторами напряжения и тока для катушки. Аналогичное соответствие между временными значениям тока и напряжения, и положениями векторов на векторных диаграммах, иллюстрируют графики для конденсатора (рис.11) и резистора (рис.12)

Законы Ома для элементов R-L-C цепей ОПТ

Математический анализ зависимости тока и напряжения на различных эле-ментах переменной цепи показывает, что для них справедлив закон Ома.

1. На резисторе закон Ома записывается точно также как и для постоянного тока - формула справедлива для любого момента времени:

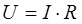
2. На катушке закон Ома соблюдается только для амплитудных значений, или для тех значений тока и напряжения, которые имеют одну и ту же фазу:

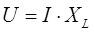где 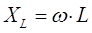- индуктивное сопротивление катушки

Из формулы следует, что сопротивление катушки тем больше, чем больше ее индуктивность и циклическая частота переменного тока. Это согласуется и с физической природой сопротивления катушки переменному току. Действительно, индуктивность L является показателем величины магнитного поля, создаваемого током (Ф = LI), а ω - показателем скорости его изменения. И то и другое в прямой пропорции увеличивают вихревую ЭДС, создающую сопротивление току.

2. На конденсаторе закон Ома также соблюдается только для амплитудных значений, или для тех значений тока и напряжения, которые имеют одну и ту же фазу:

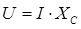, где 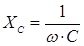- емкостное сопротивление конденсатора

В этом случае из формулы вытекает, что сопротивление конденсатора наоборот уменьшается - как с ростом частоты, таки с ростом емкости конденсатора. Это объясняется тем, что с ростом частоты заряды не успевают набежать на обкладки конденсатора и, следовательно, - создать заметное сопротивление набегающим зарядам. Рост емкости, также вызывает уменьшение сопротивления, поскольку он означает снижение, тем или иным способом, величины взаимного отталкивания зарядов.

Указанные графические методы и математические формулы позволяют перейти к описанию и анализу конкретных цепей переменного тока. Для образовательных целей наиболее принципиальными среди них являются последовательная и параллельная R-L-C-цепи.

Последовательная R-L-C цепь ОПТ

Для цепей ОПТ, как и для цепей постоянного тока, расчет сводится к определению токов и напряжений на всех участках цепи. В данном случае, при известном напряжении на генераторе (U), его циклической частоте ω, требуется определить ток в цепи (I) и напряжения на всех ее участках(U_R, U_L, U_C). Слож-ность расчета заключается в неодинако-вости фаз колебаний рассматриваемых параметров. Как уже указывалось выше, учет этих фаз можно осуществить через построение векторов.

Из схемы (рис.13) следует, что через все элементы цепи проходит один и тот же ток - следовательно, с него и надо начинать построение диаграммы. Так как в реальности все вектора вращаются, то рассмотрим схему в тот момент, когда вектор общего тока находится в горизонтальном положении и направлен вправо (рис.14): для всех последующих расчетов это не имеет никакого значения.

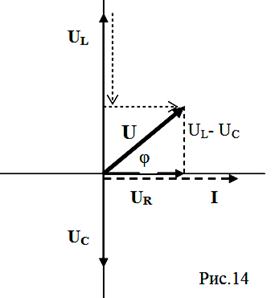
Выбор ориентации вектора тока предопределяет ориентацию напряжений на резисторе (всегда параллелен току), на катушке (направляем вверх – опережает при вращении ток) и на конденсаторе (направляем вниз - отстает при вращении от тока).

Общее напряжение на генераторе (U) получим, сложив все напряжения векторным образом, а связь между суммарным напряжением и составляющими найдем из получившегося треугольника напряжений по теореме Пифагора:

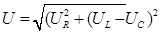
Используя законы Ома для отдельных элементов

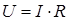
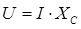
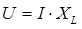
и подставляя их в полученную формулу, получим:

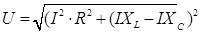
Так как ток во всех элементах одинаков, его можно вынести за квадратный корень, индуктивное и емкостное сопротивления выразить через Lи С:

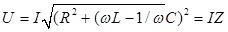
Полученное выражение можно рассматривать как закон Ома для последовательной R-L-C цепи. Параметр Zназывают полным или комплексным сопротивлением всей цепи.

Зная значение Z, нетрудно рассчитать напряжения на всех участках цепи:

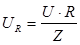
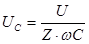
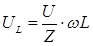
Из чертежа видно, что между векторами напряжения на генераторе и полным током существует угол φ, который по своему физическому смыслу представляет собой не что иное, как сдвиг фаз между колебаниями тока и напряжения. Из чертежа следует, что он может быть вычеслен через тангенс треугольника напряжений: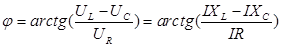

Или сокращая, ток и переходя к основным параметрам элементов, получим окончательное выражение:

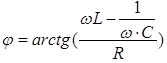
Из чертежа видно, что по модулю угол φ, в общем случае, может меняться от 0 до 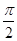. По установленным в математике правилам угол считается положительным, если он отсчитывается от горизонтальнойоси ОХ, направленной вправо, против часовой стрелки. В электротехнике сдвиг фаз считается положительным, если при вращении против часовой стрелке вектор напряжения оказывается впереди (левее) вектора тока, т.е. если напряжение опережает по фазе ток. Поскольку такое положение вещей всегда имеет место в катушке – индуктивности - то любая цепь, где напряжение опережает ток называется активно-индуктивной, а сдвиг фаз считается положительным

0 < φ <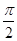

Соответственно, цепи, где ток - как и в конденсаторе - опережает напряжение называются активно–емкостными, а угол считается отрицательным

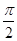- < φ < 0

В частности, если R = 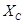=0, Z = X _L, то 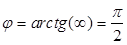- чисто индуктивная цепь; если R = =0, Z = X _с, то 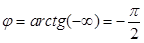- чисто емкостная цепь.

Параллельная R-L-C цепь ОПТ

Рис.15

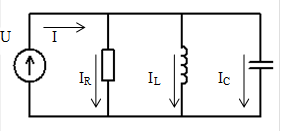
Из схемы (рис.15) видно, что при параллельном соединении все элементы цепи находятся под одним и тем же же напряжением - напряжением генератора. Следовательно, с него и надо начинать построение диаграммы (рис.16). Так как в реальности все вектора вращаются, то рассмотрим схему в тот момент, когда вектор напряжения генератора находится в горизонтальном положении и направлен вправо. Тогда фазовая ориентация векторов токов на каждом элементе будет определяться свойствами каждого элемента:

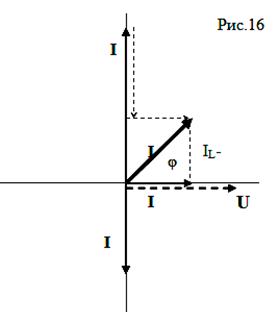
а) на резисторе вектор тока направляем параллельно напряжению - он совпадает с ним по фазе;

б) на катушке - вниз: ток отстает от напряжения;

в) на конденсаторе - вверх: ток опережает напряжение

Поскольку напряжение на всех элементах известно, то основной задачей является расчет токов (силы тока) в эле-ментах цепи и полного тока из генератора. Токи в элементах находятся непосредственно из законов Ома

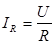
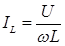
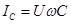
Полный ток из генератора найдем векторным сложением трех токов. Используя векторную диаграмму токов (рис.16) и складывая их по таким же правилам, что и напряжения для последовательной цепи, получим треугольник токов. Из теоремы Пифагора найдем, что:

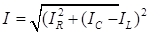
или, выражая токи через единое напряжение, и вынося далее его за скобки, получим:

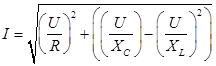
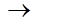
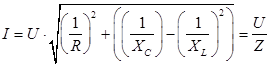
В итоге получам, так называемый, закон Ома для параллельной R-L-C цепи:

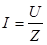
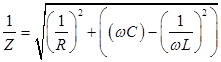
Параметр Z, как и в случае последовательной цепи представляет собой полное или комплексное сопротивление всей цепи.

Сдвиг фаз между током и напряжением найдем из треугольника токов по тангенсу этого угла.

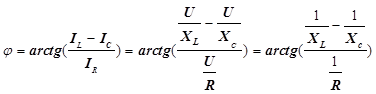
Из формулы следует, что при Х_L > Х_С угол φ оказывается отрицательным, а из векторной диаграммы - что ток при этом опережает напряжение по фазе. Это соответствует активно-емкостной цепи.

При Х_L < Х_С угол φ будет положительным, а из векторной диаграммы - что напряжение при этом опережает ток по фазе. Это соответствует активно-ин-дуктивной цепи.

Резонансные явления в цепях ОПТ

Из физики известно, что резонанс возникает в колебательных системах при дополнительном воздействии на колебательную систему внешней периодической силы. Следствием резонанса является возрастание амплитуды колебаний системы, что есстественно вытекает из самой причины явления. Действительно, резонанс возникает при совпадении колебаний внешней силы с собственными колебаниями системы. Это создает условие для односторонней перекачки энергии от внешней силы в колебательную систему с последующим возрастанием амплитуды колебаний.

1. Рассмотрим сущность резонанса в последовательной R-L-C цепи.

Математическая теория легко формулирует как причину, так и условие резонанса:

1) резонанс в последовательной цепи проявляется в значительном возрастании тока 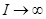в цепи, что является иной формой констатации перекачки энергии от генератора в цепь (Р= UI 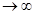-- энергия поступающая в цепь за одну секунду);

2) условие резонанса определяется из формулы:

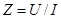или

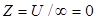
Таким образом для наступления резонанса полное сопротивление цепи должно либо равняться нулю, либо быть достаточно малым. Согласно физике такая ситуация называется режимом «короткого замыкания». Из полученных формул следует,

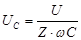
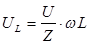
что, вследствие стремления полного сопротивления к нулю, означает рост напряжения на конденсаторе и катушке, которые при резком резонансе (R→ 0) становятся очень большими - намного больше напряжения на генераторе. Например, если генератор вырабатывает 220 в, то напряжение на катушке и конденсаторе может стать и 22 000 в. Для этого необходимо, чтобы:

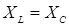или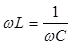

Физическая природа резонанса в последовательной R-L-C цепи связана с фазовыми сдвигами колебаний токов и напряжений.

В обычном режиме сопротивление генератору создает каждый элемент:

1) резистор - прямым торможением зарядов;

2) катушка - ЭДС электромагнитной индукцией;

3) конденсатор - взаимным кулоновским отталкиванием зарядов.

Из всех сил сопротивления самым незначительным является резистор, так как в большинстве случаев, в реальных цепях, оно сознательно делается малым - для уменьшения тепловых потерь. Следовательно, реальное сопротивление генератору оказывают катушка и конденсатор. Однако, при одном и том же токе в катушке и конденсаторе, их напряжения всегда находятся в противофазе. Это значит, что каждый из них гасит не только напряжение генератора, но и своего «соседа» по цепи.

Например, если катушка запасает больше энергии, чем конденсатор, то ее напряжение противостоит и напряжению генератора и напряжению конденсатора. Если конденсатор запасает больше, - то наоборот. Однако если запасаемые ими энергии оказываются одинаковыми, то генератор не встречает никакого сопротивления ни со стороны катушки ни со стороны генератора, т.к они полностью подавляют друг друга. В этом случае единственной тормозящей силой току из генератора становится только резистор - если он имеется в цепи.

2. В параллельной R-L-C цепи возникает явление, которое называют резонансом токов.

Математически резонанс формулируется следующим образом:

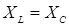или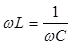

т.е. точно так же, как и резонанс напряжений. Однако физические проявления этого резонанса оказываются менее выраженными.

Действительно, из условия 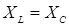следует, что 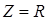. Это означает, что все токи и напряжения при выполнении математического условия резонанса остаются конечными. Отчетливые признаки того, что принято называть резонансом токов, возникают в случае, когда резистор из цепи удаляется - формально-математически это означает 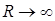. В этом случае из 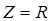следует 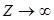, а из этого, в свою очередь, .

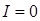Физически это означает прекращение поступления тока от генератора в цепь. Вместе с тем, в самой цепи продолжают циркулировать токи, - причем сколь угодно большой величины. Это следует из того что оставшиеся элементы цепи – катушка и конденсатор - оказываются под полновесным напряжением генератора и в них протекают токи, равные:

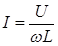и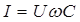

Причина такого явления, опять таки связана с расфазировкой, только теперь уже токов. Ранее уже говорилось, что напряжения конденсатора и катушки при резонансе в последовательной цепи, при одном и том же токе, противофазны. В параллельной цепи возникает обратная ситуация: при одном и том же напряжении противофазны токи. То есть когда ток из катушки вытекает, в конденсаторе наоборот, – он втекает. При соблюдении условия 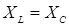, токи становятся совершенно одинаковыми и весь ток, уходящий из конденсатора, целиком поступает в катушку. Напряжение, при этом, в обоих элементах одинаково и противофазно напряжению генератора, что «запирает» для него всю цепь. Следовательно, в таких условиях возникает явление противоположное «классическому» резонансу - прекращение поступления энергии от внешнего источника в колебательную систему. Тем не менее, в литературе это явление называется резонансом, имея ввиду возникновение в цепи свободных колебаний без участия генератора.

Энергетические процессы в цепях ОПТ

Энергетические процессы в цепях ОПТ описываются теми же формулами мощности (Р) и энергии (W), что и в цепях постоянного тока.

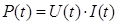
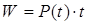
Однако для конкретных выводов и физического анализа эти формулы непригодны, так как не учитывают особенностей переменного тока, в частности, - структуры его энергии. Будем отсчитывать все фазы от напряжения. Тогда мощность, поступающую в цепь целесообразно разделить на реактивную и активную. Смысл этого разделения вытекает из разной природы этих мощностей. Активная мощность безвозвратно поглощается в резисторах, тогда как реактивная сохраняется. Такое разделение столь же важно и необходимо, как разделение работы и теплоты в термодинамике.

1. С учетом сказанного, вычислим мощность поглощаемую цепью - она задается активной составляющей тока:

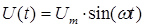и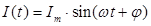

Тогда, подставляя, получим: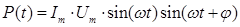

Из алгебры известна формула: 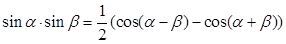, так что:

= =

= =

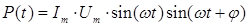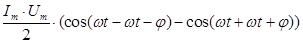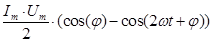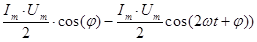
Последнее выражение обнаруживает, что общая формула 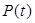содержит постоянную

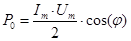и - переменную 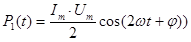составляющие.

	Рис.17

 

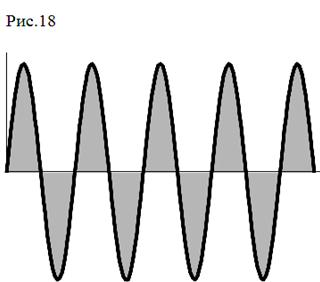
С физической точки зрения, первая составляющая выражает мощность, непрерывно поступающую и поглощаемую цепью. Действительно, только эта составляющая энергии ежесекундно увеличивается по значению. Переменная же составляющая с течением времени не растет всле-дствие знакопеременности. Слева (рис.17, рис.18) приведены графики измене-ния мощности при φ = 0 и φ = π/2

Из них следует, что при φ = 0 вся мощность Р(t) положительна и,следовательно, только поглощается. Этот режим соответствует чисто резистивной цепи. При φ = π/2 половина времени мощность Р(t) положительна, половина отрица-тельна. Это означает, что суммарная мощность, поступающая в сеть равна нулю.

Из теории постоянного тока известно, что мощность может быть отрицательной только в случаях, когда ток течет против ЭДС источника, а это, в свою очередь, возможно только тогда, когда в цепи не один, а несколько источников тока. Полученная выше отрицательная мощность объясняется наличием в це-пи переменного тока катушек и конденсаторов, которые способны возвращать, т.е. генерировать, запасенную ранеее энергию. Именно они, в определенные мо-менты времени, направляют ток против напряжения генератора.

2. Рассмотрим теперь зависимость от времени реактивной мощности. Она вычисляется через реактивную составляющую тока, так как только чистоемкостной или чисто индуктивный ток возвращают энергию генератору.

Исходные уравнения для расчета имеют вид:

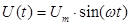и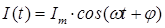

Здесь принято во внимание, что реактивный ток отличается по фазе по отношению к напряжению на 90⁰ (положительный знак φ означает, что формула для тока непосредственно описывает активно-емкостную цепь; для активно-индуктивной цепи φ надо взять со знаком «-»). Тогда обозначая непоглощаемую, т.е. реактивную мощность буквой Q, запишем:

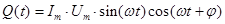
Далее используем известную алгебраическую формулу:

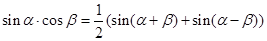
или

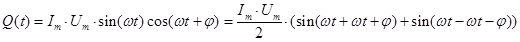
Таким образом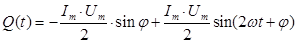

Аналогичным образом формула мощности содержит постоянную 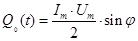(знак «-» связан с выбором опережающего характера тока) и переменную 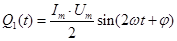составляющие.

Так как переменные составляющие не представляют интереса, мы приходим окончательно к двум важнейшим формулам мощности переменного тока:

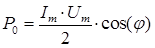и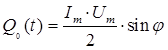

Учитывая известное выражение 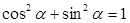, введем понятие полной мощности переменного тока:

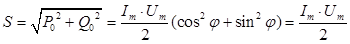
Из формул следует что реальные мощности оказываются в 2 раза меньше максимально возможных. В связи с этим в электротехнике введены понятия действующих значений тока и напряжения:

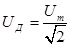и ;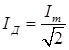

тогда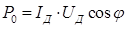

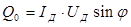
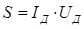
Во всех дальнейших формулах подразумеваются только действующие значения токов и напряжений и индексы при них не ставятся.