Ряд Фурье для четных и нечетных функций

 

Отметим следующие свойства четных и нечетных функций:

v Лемма1

1)

Доказательство

можно получить из интерпретации интеграла как площади для четной и нечетной функции

v Лемма 2 Произведение двух четных и нечетных функций является четной функцией.

v Лемма 3 Произведение четной и нечетной функций – нечетная функция.

Справедливость этих свойств может быть легко доказана исходя из определения четности и нечетности функций.

Функция - четная функция, если - четная, то - четная, а 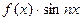- нечетная.

Если f(x) – четная периодическая функция с периодом , удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:

Таким образом, для четной функции ряд Фурье записывается:

Аналогично получаем разложение в ряд Фурье для нечетной функции:

_.

 

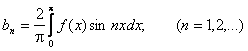q Пример. Разложить в ряд Фурье периодическую функцию с периодом T = на отрезке .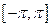

Решение

Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:

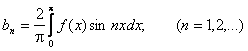
Получаем:

.

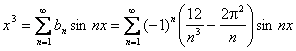Построим графики заданной функции и ее разложения в ряд Фурье, ограничившись первыми четырьмя членами ряда.

 

 

1.7 Ряды Фурье для функций любого периода

 

Предположим, что функция f задана в промежутке [- l, l ], где l -- некоторое положительное число. Сделав подстановку

получим функцию 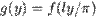,определенную в промежутке

Функции g соответствует (формальный) ряд Фурье

коэффициенты которого находятся по формулам Эйлера -- Фурье:

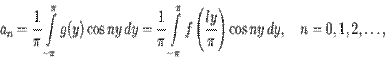
Возвращаясь к старой переменной, т.е. полагая в выписанных формулах ,мы получим для функции f тригонометрический ряд несколько измененного вида:

где

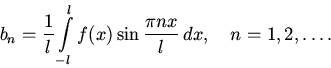
Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [- l, l ].

Для четной функции произвольного периода разложение в ряд Фурье имеет вид:

Для нечетной функции:

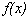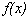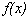ü Замечание. Если непериодическая кусочно-гладкая функция задана лишь в интервале , ее тоже можно разложить в ряд Фурье. Полученный ряд будет сходиться на всей числовой оси, но к функции только в тех точках интервала , в которых функция непрерывна.

ü Суммой ряда будет периодическое продолжение функции 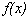на всю ось Ox. А в точках разрыва сумма ряда будет равна среднему арифметическому правого и левого пределов периодического продолжения данной функции.

В случае, когда 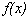задана на произвольном интервале (a; b), обозначим 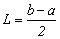, зададим конкретное значение функции на одном из концов интервала (например, при x = b) и продолжим данную функцию периодически, с периодом T = 2L на всю числовую ось. Полученная функция будет удовлетворять условиям теоремы Дирихле.

Коэффициенты ряда Фурье в этом случае можно определить следующим образом:

тогда ряд Фурье принимает вид

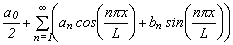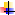Пример. Разложить функцию

в ряд Фурье в интервале (2; 6).

Решение

Данная функция является кусочно-монотонной и непрерывной в заданном интервале. Доопределим ее и продолжим функцию , заданную для 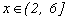периодически, с периодом T = 2L = 4 на всю числовую ось. Полученная функция будет удовлетворять условиям теоремы Дирихле.

Коэффициенты ряда Фурье можно определить следующим образом:

;

;

;

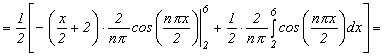
Тогда ряд Фурье для данной функции имеет вид:

.

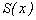Полученный ряд будет сходиться на всей числовой оси, но к функции только в точках . Суммой ряда будет периодическое продолжение функции на всю ось Ox. А в точках разрыва сумма ряда

, где - точки разрыва функции .

Ответ: .

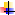Пример Разложить в ряд Фурье функцию с периодом 2π, если в интервале , продолжив ее на интервале четным или нечетным образом.

Решение

Найдём разложение функции в ряд Фурье для различных продолжений исходной функции:

а) доопределим функцию на интервале . Полученная функция будет четной. Продолжим её периодически, с периодом T = 2L = 2π на всю числовую ось. В результате полученная функция будет удовлетворять условиям теоремы Дирихле.

 

Таким образом, для полученной четной функции:

; ;

Отличны от нуля только коэффициенты с нечетными индексами .

Тогда ряд Фурье для данной функции имеет вид:

.

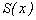Найденное разложение имеет место при всех значениях , однако ряд, стоящий справа, сходится при всех x. Суммой ряда будет периодическое продолжение функции на всю ось Ox.

Ответ: ;

 

б) аналогично предыдущему случаю строим нечетное, 2π - периодическое продолжение исходной функции. Доопределим функцию на интервале . Положим для простоты .

Коэффициенты Фурье:

;

.

Для всех x = π + 2πn .

Тогда ряд Фурье для данной функции имеет вид:

.

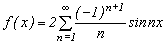Найденное разложение имеет место при всех значениях , однако ряд, стоящий справа, сходится при всех x. Суммой ряда будет периодическое продолжение функции на всю ось Ox. А в точках разрыва сумма ряда

,

где - точки разрыва функции .

Ответ: .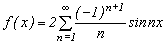

 

Интеграл Фурье

 

роль интеграл Фурье играет в электротехнических задачах.

Пусть функция f (x) задана на всей числовой прямой, на промежутке удовлетворяет условиям Дирихле

v Теорема Для того, чтобы f (x) была представлена интегралом Фурье во всех точках непрерывности и правильных точках разрыва, достаточно:

1) абсолютной интегрируемости, т.е. 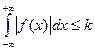(т.е. интеграл сходится)

2) на любом конечном отрезке [- L, L ] функция была бы кусочно-гладкой

3) в точках разрыва функции, ее интеграл Фурье определяется полусуммой левого и правого пределов в этих точках, а в точках непрерывности к самой функции f (x),

тогда интегралом Фурье функции f(x) называется интеграл вида:

,

где

, .

Или в виде

.

Эта формула впервые встречается при решении некоторых задач теплопроводности у Ж. Фурье (1811), но её доказательство было дано позже другими математиками.

Это можно рассматривать как предельную форму ряда Фурье для функций, имеющих период 2 T.

При этом а (u) и b (u) аналогичны коэффициентам Фурье функции f (x).

 

1.9 Интеграл Фурье для четной и нечетной функции

 

Представление непериодической функции интегралом Фурье упрощается, если функция обладает симметрией.

Пусть f (x)-четная функция, удовлетворяющая условиям представимости интегралом Фурье.

Таким образом, интеграл Фурье четной функции f (x) запишется так:

,

где a (u) определяется равенством

Рассуждая аналогично, получим интеграл Фурье для нечетной функции f (x)

,

 

ü Замечание Характерной чертой, отличающей интеграл Фурье от ряда Фурье, является то, что ряд Фурье это периодическая функция как сумма периодических составляющих, а интеграл Фурье – непериодическая функция.

 

1.10 Комплексная форма интеграла Фурье

 

Интеграл Фурье в комплексной форме

,

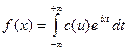где

.

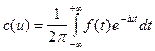Если в формуле заменить c (u) его выражением, то получим:

,

где правая часть формулы называется двойным интегралом Фуpье в комплексной форме.

Переход от интеграла Фурье в комплексной форме к интегралу в действительной форме и обратно осуществим с помощью формул:

Формулу можно преобразовать также к виду

(простой интеграл Фурье).

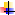Пример: разложить в ряд Фурье в комплексной форме.

Решение

Функция периодическая с периодом .(f(x+T)=f(x))

Функция имеет на промежутке конечное число точек разрыва первого рода.

Сумма ряда в точках функции сходится к значению самой функции, а в точках разрыва к величине , где -точки разрыва.

 

Запишем комплексную форму полученного ряда

,

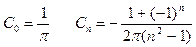но при не существует, поэтому рассмотрим случай когда n =+1:

(т.к. см. разложение выше)

и случай когда n =-1:

(т.к. )

 

И вообще комплексная форма:

или

или

 

1.11 Преобразование Фурье

 

Преобразование Фурье, первоначально возникло в теории теплопроводности, имеет многочисленные применения как в самой математике (например, при решении дифференциальных, разностных и интегральных уравнений, в теории специальных функций и т.д.), так и в различных разделах теоретической физики. Например, преобразование Фурье стало стандартным аппаратом квантовой теории поля, широко используется в методе функций Грина для неравновесных задач квантовой механики и термодинамики, в теории рассеяния и т.д.

Ø Определение Преобразование Фурье - функция, выражающаяся через данную функцию f (x) формулой:

,

Если функция f (x) чётная, то её преобразование Фурье равно

(косинус-преобразование),

а если f (x) — нечётная функция, то

(синус-преобразование).

Формулы (1), (2) и (3) обратимы, т. е. для чётных функций

,

а для нечётных функций

.

В общем случае имеет место формула

.

Глава 2 Математическая логика и ИВ

 

Своим существованием наука «алгебра логики» обязана английскому математику Джорджу Булю, который исследовал логику высказываний. Первый в России курс по алгебре логики был прочитан Б. Порецким в Казанском государственном университете.

Как самостоятельная наука логика оформилась в трудах греческого философа Аристотеля (384-322 г.г до н.э.). Он систематизировал известные до него сведения, и эта система стала впоследствии называться формальной или Аристотелевой логикой.

Формальная логика просуществовала без серьёзных изменений более двадцати столетий. Естественно, что развитие математики выявило недостаточность Аристотелевой логики и потребовало дальнейшего её развития.

Впервые в истории идеи о построении логики на математической основе были высказаны немецким математиком Г. Лейбницем (1646-1716) в конце XVII века. Он считал, что основные понятия логики должны быть обозначены символами, которые соединяются по особым правилам. Это позволит всякое рассуждение заменить вычислением.

“Мы употребляем знаки не только для того, чтобы передать наши мысли другим лицам, но и для того, чтобы облегчить сам процесс нашего мышления” (Лейбниц).

Первая реализация идеи Лейбница принадлежит английскому учёному Д. Булю (1815-1864). Он создал алгебру, в которой буквами обозначены высказывания, и это привело к алгебре высказываний. Введение символических обозначений в логику имело для этой науки такое же решающее значение, как и введение буквенных обозначений для математики. Именно благодаря введению символов в логику была получена основа для создания новой науки – математической логики.

Применение математики к логике позволило представить логические теории в новой удобной форме и применить вычислительный аппарат к решению задач, малодоступных человеческому мышлению, и это, конечно, расширило область логических исследований.

Одной из основных причин развития математической логики является широкое распространение аксиоматического метода в построении различных математических теорий.

На практике множество элементарных логических операций является обязательной частью набора инструкций всех современных микропроцессоров и соответственно входит в языки программирования. Это является одним из важнейших практических приложений методов математической логики.

Перед изучением основ математической логики необходимо рассмотреть понятие логики в целом.

Logos (греч.) - слово, понятие, рассуждение, разум.

Слово ”логика” обозначает совокупность правил, которым подчиняется процесс мышления или обозначает науку о правилах рассуждения и тех формах, в которых оно осуществляется.

Логика изучает абстрактное мышление как средство познания объективного мира, исследует формы и законы, в которых происходит отражение мира в процессе мышления.

Рассмотрим вкратце историю развития логики.

 

 

2.1 Этапы развития логики

1-й этап связан с работами ученого и философа Аристотеля (384-322 гг. до н.э.). Он пытался найти ответ на вопрос ”как мы рассуждаем”, изучал ”правила мышления”.

Аристотель впервые дал систематическое изложение логики. Он подверг анализу человеческое мышление, его формы - понятие, суждение, умозаключение и рассмотрел мышление со стороны строения, структуры, то есть с формальной стороны. Так возникла формальная логика.

Формальная логика связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным языком. Аристотель исследовал различные формы рассуждений и их комбинаций, ввел понятие силлогизма, т.е. рассуждения, в котором из заданных двух суждений выводится третье.

Теория правильных рассуждений, которая называлась силлогистикой и метод вывода правильных заключений из посылок – дедукция были сформированы более 2 тысяч лет тому назад, никем не опровергнуты и считаются присущими человеческому мышлению.

ü Замечание Не путать с "дедуктивным методом" Шерлока Холмса. У Холмса, или скорее у Конан-Дойля, явно были проблемы с логикой, коль скоро он путал дедукцию с индукцией... ДЕДУКТИВНЫЙ подход, называемый еще АКСИОМАТИЧЕСКИМ, это подход от общего к частному. От аксиом (постулатов) к теоремам (следствиям).

Пример:

Все квадраты – ромбы → все ромбы - параллелограммы→Следовательно, все квадраты - параллелограммы.

В общем виде этот силлогизм имеет форму: ”Все а суть в, все в суть с. Следовательно, все а суть с. ”

Пример Силлогизм неправильной формы:

Все квадраты - ромбы. →Некоторые ромбы имеют острый угол. →Следовательно, некоторые квадраты имеют острый угол.

Значит, силлогизм, имеющий форму ”Все а суть в, некоторые в суть с. Значит, некоторые а суть с ” может привести и к ложным выводам.

Аристотель выделил все правильные формы силлогизмов, которые можно составить из рассуждений вида:

- 1. "Все а суть в"

- 2. "Некоторые а суть в"

- 3. "Все а не суть в"

- 4. "Некоторые а не суть в"

Ø Определение Логика, основанная на теории силлогизмов называется классической.

Доказано, что общее число силлогизмов, которые можно составить из рассуждений указанного вида, равно 256, из них правильными являются лишь 24.

В конце XVI в. в алгебре словесная форма записи алгебраических выражений стала тормозить развитие науки и, чтобы облегчить выполнение алгебраических преобразований, была создана буквенная символика, позволяющая выполнять эти преобразования по строго определенным правилам.

2-й этап - появление математической или символической логики. Основы ее заложил немецкий ученый и философ Готфрид Вильгельм Лейбниц (1646-1716). Он попытался построить первые логические исчисления, считал, что можно заменить простые рассуждения действиями со знаками и привел правила. Но Лейбниц высказал только идею, а развил ее окончательно англичанин Джордж Буль (1815-1864). Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику. Недаром начальный раздел математической логики называют алгеброй логики, или булевой алгеброй.

3-й этап связан с XX веком и попытками обосновать справедливость математических доказательств, с исследованиями теории чисел, а также с попыткой разрешить известные логические парадоксы.

Парадокс лжеца

Самым знаменитым следует считать парадокс лжеца, известный еще со времен глубокой древности.

По преданию, Эпименид утверждал, что все критяне лжецы. Верно ли это утверждение, если учесть, что сам Эпименид родом с острова Крит?

Другая простейшая форма этого парадокса:

«Некто говорит: ’’я лгу’’.

Если он при этом лжет, то сказанное им есть ложь, и, следовательно он не лжет.

Если же он не лжет, то сказанное им есть истина, и следовательно, он лжет.

В любом случае оказывается, что он «лжет и не лжет одновременно»