Разложение в ряд Фурье непериодической функции

Федеральное государственное бюджетное образовательное учреждение высшего образования

«ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ»

Кафедра высшей математики

 

 

О.В.СТАРОЖИЛОВА

 

 

СПЕЦИАЛЬНЫЕ ГЛАВЫ МАТЕМАТИКИ

 

Самара,

УДК 512.6, 514.1

Рекомендовано к изданию методическим советом ПГУТИ,

протокол № 45, от 10.03.2017 г.

 

Старожилова, О.В.

С Специальные главы математики: учебное пособие //Старожилова О.В.. – Самара: ПГУТИ, 2017. –221 с.

 

Учебное пособие затрагивает специальные разделы математики: математическая логика и теории автоматов, алгебра высказываний, исчисление высказываний, элементы теории алгоритмов, регрессионный анализ, методы оптимизации.

Для студентов и магистров университета, обучающихся по направлению 09.03.02 «Информационные системы и технологии», желающих изучать специальные главы математики самостоятельно.

Каждый раздел заканчивается контрольными вопросами, которые помогут проверить теоретическое освоение курса, содержит большое количество задач для самостоятельного решения и ответы для проверки.

Пособие содержит лабораторный комплекс и ряд инженерных задач с акцентом на программную реализацию методов вычислительной математики.

 

 

Старожилова О.В., 2017

 

Оглавление

Глава 1 Гармонический анализ 6

1.1 Задача о звучащей струне 7

1.2 Ортогональные системы функций 8

1.3 Ряд Фурье по тригонометрической системе функций 10

1.4 Достаточные условия разложения функции в ряд Фурье 13

1.5 Разложение в ряд Фурье непериодической функции 17

1.6 Ряд Фурье для четных и нечетных функций 18

1.7 Ряды Фурье для функций любого периода 21

1.8 Интеграл Фурье 27

1.9 Интеграл Фурье для четной и нечетной функции 29

1.10 Комплексная форма интеграла Фурье 30

1.11 Преобразование Фурье 32

Глава 2 Математическая логика и ИВ 33

2.1 Этапы развития логики 34

2.2 Логика высказываний 38

2.3Логические связки 40

2.4Логические операции 41

2.5 Алфавит исчисления высказываний 42

2.6 Формулы.Тавтология 42

2.7Законы логики высказываний 44

2.8 Формальные теории. Выводимость. Интерпретация 46

2.9 Аксиоматический метод 47

2.10 Система аксиом исчисления высказываний (ИВ) 52

2.11 Правила вывода 53

2.12 Производные правила вывода 56

2.13 Построение вывода в логике высказываний 62

2.14 Связь между алгеброй и исчислением высказываний 66

Контрольные вопросы 69

Глава 3 Задачи регрессионного анализа 70

3.1 Метод наименьших квадратов 74

3.2 Линейный регрессионный анализ 76

3.3 Оценка модели регрессии 79

3.4 Проблемы применения метода линейной регрессии 83

3.5 Предпосылки статистической модели ЛР 85

3.6 Задачи регрессионного анализа 86

3.7 Многомерная нормальная регрессионная модель 90

3.8 Вариация зависимой переменной 92

Контрольные вопросы 94

Глава 4 Общая постановка и виды задач принятия решений 95

4.1 Математическая постановка задачи оптимизации 97

4.2Локальный и глобальный минимум ЦФ 99

4.3 Методы безусловной оптимизации 102

4.4 Метод покоординатного спуска 102

4.5 Метод Розенброка 105

4.6 Метод конфигураций 105

4.7 Методы случайного поиска 108

4.8 Метод Ньютона 112

Глава 5 Преобразование Фурье 114

5.1 Аппрокисмация функции по Фурье 114

5.2 Преобразование Фурье 117

5.3 Быстрое преобразование Фурье 120

ЛАБОРАТОРНЫЙ КОМПЛЕКС 123

Гармонический и спектральный анализ 123

Тема 1. «Логика высказываний» 131

Варианты индивидуальных заданий темы ЛВ 133

Тема 2. Линейная парная регрессия 140

Лабораторная работа № 1 141

Вычисление коэффициентов уравнения ЛР 141

Лабораторная работа № 2 144

Вычисление выборочного коэффициента корреляции 144

Лабораторная работа № 3 145

Вычисление оценок дисперсий парной ЛР 145

Лабораторная работа №4 147

Функции Excel для коэффициентов парной ЛР 147

Лабораторная работа № 5 149

Построение интервальной оценки для функции парной ЛР 149

Лабораторная работа № 6 151

Проверка значимости уравнения ЛР по критерию Фишера 151

Тема 3 Нелинейная парная регрессия 153

Лабораторная работа № 7 153

Построение нелинейной регрессии с использованием 153

Команды «Добавить линию тренда» 153

Лабораторная работа № 8 158

Выбор наилучшей нелинейной регрессии 158

Тема 4. Линейная множественная регрессия 161

Лабораторная работа № 9 162

Вычисление коэффициентов ЛМР 162

Лабораторная работа № 10 166

Проверка значимости в режиме Регрессия 166

Тема 5. Нелинейная множественная регрессия 175

Лабораторная работа № 11 175

Вычисление для функция Кобба-Дугласа 175

Контрольная работа № 1 179

Парная регрессия 179

Контрольная работа № 2 181

Множественная линейная регрессия 181

Численные методы поиска безусловного экстремума 185

Графический анализ функции 185

Задача одномерного поиска 187

Алгоритм Свенна 190

Метод перебора 193

Метод поразрядного поиска 195

Метод дихотомии. 198

Метод Фибоначчи 201

Метод золотого сечения 205

Метод средней точки 210

Метод Ньютона 214

Вывод 216

Литература 218

 

 

Глава 1 Гармонический анализ

Определение Гармонический анализ- разделматематики, связанный с разложением колебаний на гармонические колебания.

При изучении периодических (т. е. повторяющихся во времени) явлений рассматриваются периодические функции.

Например, гармоническое колебание описывается периодической функцией времени t:

Ø Определение Периодическая функция - функция, значение которой не изменяется при добавлении к аргументу определённого, неравного нулю числа, называемого периодом функции.

Так как сумма и разность двух периодов есть снова период и, следовательно, любое кратное периода есть также период, то каждая периодическая функция имеет бесконечное множество периодов.

Если периодическая функция имеет действительный период, непрерывна и отлична от постоянной, то для неё существует наименьший положительный период Т; всякий другой действительный период той же функции будет иметь вид kT, где k = ±1, ± 2,....

Сумма, произведение и частное периодических функций с одним и тем же периодом являются периодическая функция с тем же периодом.

Периодические функции играют чрезвычайно большую роль в теории колебаний и вообще в математической физике. В курсе математического анализа знакомились с понятием функционального ряда , работали с его важным частным случаем - степенным рядом . Рассмотрим другой очень важный (в том числе и для физических приложений) частный случай функциональных рядов -- тригонометрический ряд.

Ø Определение Функциональный ряд – ряд вида

,

где 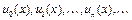- функции, зависящие от одной переменной или от нескольких переменных.

При каждом фиксированном значении функциональный ряд превращается в числовой ряд

который может сходиться, а может и расходится.

Ø Определение Точка сходимости функционального ряда - точка , в которой функциональный ряд сходится.

Ø Определение Множество всех точек сходимости называется областью сходимости ряда.

Можно ли данную функцию 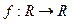представить в виде тригонометрического ряда, т.е. можно ли найти коэффициенты a_n и b_n такие, что для всех имеет место равенство

 

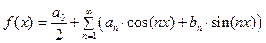
Сумма ряда очевидно, -периодическая функция. Значит, разлагать в тригонометрический ряд можно только периодические функции f.

Кроме того ясно, что если две периодические функции совпадают на промежутке, длина которого равна периоду, то они совпадают всюду. Поэтому достаточно проверить на некотором промежутке длины , например, .

 

1.1 Задача о звучащей струне

 

К изучению тригонометрических рядов привела поставленная в 18 веке задача о звучащей струне.

Дана функция , можно ли найти тригонометрический ряд, который сходится и имеет своей суммой функцию . На необходимо наложить ограничения, чтобы можно было искать сходящийся к ней тригонометрический ряд.

Аналогичная задача была для степенных рядов, если она разрешима, то таким рядом является ряд Тейлора.

 

 

 

1.2 Ортогональные системы функций

 

Систематическое изучение ортогональных систем функций было начато в связи с методом Фурье решения краевых задач уравнений математической физики. Одна из основных задач теории ортогональных систем функций — задача о разложении функции f (x) в ряд вида 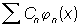, где ортогональная система функций.

Ø Определение Функции и 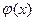называются ортогональными на , если выполняется:

q Пример 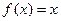, 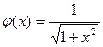- функции ортогональны на 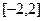, т.к.

q Пример 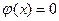на ортогональна к любой, определенной на функции.

 

Ø Определение Бесконечная система функций называется ортогональная на , если

q Пример Бесконечная система функций 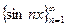на образует ортогональную на систему функций

.

 

 

q Пример 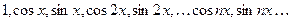- тригонометрическая система функций образует ортогональную на систему функций.

, , .

 

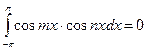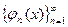Ø Определение Пусть задана произвольная ортогональная на система функций . Ряд

,

где - произвольные числовые коэффициенты, называется рядом по ортогональной системе функций.

Ø Определение Ряд по тригонометрической системе функций

называется тригонометрическим рядом.

 

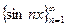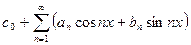ü Замечание Если - сумма тригонометрического ряда, сходящегося в каждой точке, то она периодическая, так как , - периодические функции с периодом ,то в равенстве ничего не изменится, следовательно периодическая.

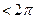ü Замечание Если задана на отрезке , но не , то сдвигом начала координат можно свести к изученному случаю.

ü Замечание Если периодическая функция с периодом ,не , то ее разлагают в тригонометрический ряд

q Теорема Если сходится числовой ряд , то тригонометрический ряд

сходится абсолютно и равномерно на всей оси .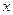

Доказательство

Следовательно,

ряд - мажорирует данный тригонометрический ряд, по признаку Вейерштрасса сходится равномерно.

Абсолютная сходимость очевидна.

 

 

1.3 Ряд Фурье по тригонометрической системе функций

 

Жан Батист Жозеф Фурье 1768 – 1830 – французский математик.

Для вычисления коэффициентов ряда Фурье вычислим интегралы

Если

, ,

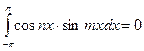Если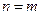

, ,

q Теорема Если для всех 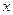имеет место равенство

и тригонометрический ряд сходится равномерно на всей оси, то коэффициенты этого ряда определяются

, ,

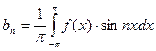
Доказательство

Ряд сходится равномерно на всей числовой оси, его членами являются непрерывные функции, то его сумма тоже непрерывна и возможно почленное интегрирование ряда в пределах

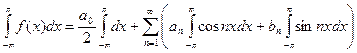
Каждый интеграл равен нулю, т.к. тригонометрическая система функций ортогональна на , а , то

Для доказательства умножим обе части на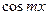

Это не нарушит равномерной сходимости ряда.

В силу равномерной сходимости ряда

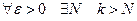
а это и означает сходимость равномерную ряда.

Интегрируя на , имеем

В силу ортогональности тригонометрической системы функций на

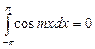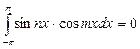, , а из отличен интеграл при ,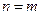

Итак

, что и т.д.

Запомним, что

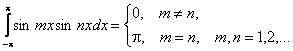
Справедливость этих равенств вытекает из применения к подынтегральному выражению тригонометрических формул.

Формула для 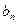доказывается аналогично.

 

ü Замечание Теорема остается справедливой на любом отрезке , при этом пределы интегрирования заменяются соответственно на и .

 

 

Ø Определение Тригонометрический ряд

,

коэффициенты которого определяются по формулам

, ,

,

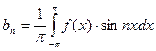называется рядом Фурье для функции , а коэффициенты называются коэффициенты Фурье.

Если ряд Фурье функции f(x) сходится во всех ее точках непрерывности, то говорят, что функция f(x) разлагается в ряд Фурье.

ü Замечание Не всякий тригонометрический ряд является рядом Фурье, даже, если он сходится на всей числовой прямой.

Сумма неравномерно сходящегося ряда может быть разрывной и не интегрируемой, поэтому определение коэффициентов Фурье невозможно.

 

ü Замечание Ряд Фурье является частным случаем функциональных рядов.

 

1.4 Достаточные условия разложения функции в ряд Фурье

 

Ø Определение Функция называется кусочно-монотонной на отрезке [a,b], если этот отрезок можно разбить конечным числом точек x₁, x₂,..., x_n-1 на интервалы (a, x₁), (x₁, x₂),..., (x_n-1, b) так, что на каждом из интервалов функция монотонна, т. е. либо не возрастает, либо не убывает.

 

ü Замечание Из определения следует, что если функция кусочно-монотонная и ограничена на [ a, b ], то имеет разрывы только первого рода.

Ø Определение Функция называется кусочно-гладкой, если на каждом конечном интервале она и ее производная имеют не более конечного числа точек разрыва 1-го рода.

q Теорема (условие Дирихле достаточное условие разложимости функции в ряд Фурье):Если периодическая функция с периодом удовлетворяет одному из условий:

1)	кусочно-гладкая, на отрезке ,
2)	кусочно-монотонная и ограничена,

то ряд Фурье, построенный для этой функции, сходится во всех точках

и сходится к числу в каждой точке ее разрыва.

Сумма полученного ряда равна значению функции в точках непрерывности функции

 

_,

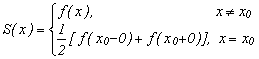где x₀ - точка разрыва функции. .

 

ü Замечание В ряд Фурье можно разложить и непериодическую функцию, при этом полученный ряд будет сходиться к функции только в тех точках интервала, в которых функция непрерывна.

ü Полученный ряд будет сходящимся на всей числовой прямой, а его сумма будет периодическим продолжением функции на всю ось, исключение лишь точки разрыва, в которых сумма ряда будет равна средне арифметическому правого и левого пределов периодического продолжения данной функции.

 

 

q Пример Разложить в ряд Фурье

 

Решение

Данная функция является кусочно-гладкой в интервале , а ее периодическое продолжение при дополнительном условии , 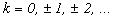удовлетворяет всем условиям теоремы Дирихле.

Вычислим коэффициенты Фурье, используя формулы (2):

;

^,

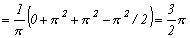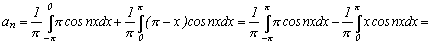
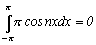так как подынтегральная функция четная, а 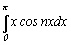вычисляем с помощью интегрирования по частям, где U = x, dU = dx, =

;

^,

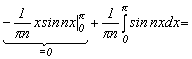
так как подынтегральная функция нечетная, а вычисляем с помощью интегрирования по частям, где

=

^.

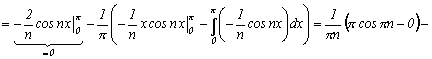
Подставим найденные коэффициенты, тогда ряд Фурье для данной функции имеет вид:

.

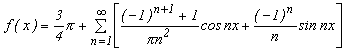Полученный ряд будет сходиться на всей числовой оси, но к функции только в точках .

Суммой ряда 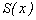будет периодическое продолжение функции на всю ось Ox

в точках разрыва сумма ряда

,

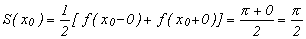где - точки разрыва функции .

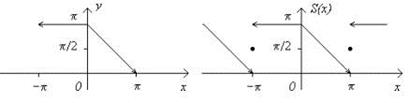
Ответ: _.

 

Этот ряд содержит бесконечное число косинусных или синусных составляющих - гармоник, причем амплитуды этих составляющих являются коэффициентами Фурье.

Помимо упомянутой формы ряд Фурье можно представить в виде

где амплитуда А_k и фаза гармоник определяются выражениями:

ü Замечание Гармоническим анализом называют разложение функции f (t), заданной на отрезке [0, Т] в ряд.

 

ü Замечание Гармоническим синтезом называют получение колебаний сложной формы путем суммирования их гармонических составляющих (гармоник).

 

Разложение в ряд Фурье непериодической функции

 

Пусть функция f(x) задана на отрезке [a, b] и является на этом отрезке кусочно–монотонной. Рассмотрим произвольную периодическую кусочно–монотонную функцию f₁(x) c периодом 2Т, совпадающую с функцией f(x) на отрезке [a, b].

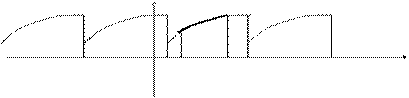
Таким образом, функция f(x) была дополнена. Теперь функция f₁(x) разлагается в ряд Фурье.

Сумма этого ряда во всех точках отрезка [a,b] совпадает с функцией f(x), т.е. можно считать, что функция f(x) разложена в ряд Фурье на отрезке [a,b].

Таким образом, если функция f(x) задана на отрезке, равном ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем , то функция продолжается на интервал (b, a + ) так, что условия разложимости в ряд Фурье сохранялись.

ü Замечание Продолжение заданной функции на отрезок (интервал) длиной может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке [a,b].