Парадокс Рассела брадобрея

Владелец парикмахерской в одном селе повесил следующее объявление: "Брею тех и только тех жителей села, кто не бреется сам". Спрашивается, кто бреет брадобрея?

Развитие математической логики особенно активизировалось в XX нашего века в связи с развитием вычислительной техники и программирования.

Ø Определение Математическая логика - это современная форма логики, которая полностью опирается на формальные математические методы. Она изучает только умозаключения со строго определенными объектами и суждениями, для которых можно однозначно решить, истинны они или ложны.

Основным (неопределяемым) понятием математической логики является понятие «простого высказывания». Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным.

Ø Определение Высказывание - это повествовательное предложение, о котором можно сказать, что оно истинно или ложно.

Высказывания могут быть истинными И или ложными Л.

Пример: Земля - планета Солнечной системы. (Истинно); Каждый параллелограмм есть квадрат (Ложно)

Существуют высказывания, о которых нельзя говорить с уверенностью, истинны они или ложны. «Сегодня хорошая погода»(кому как)

Пример Высказывание "Идет дождь" - простое, а истинное оно или ложное зависит от того, какая погода сейчас за окном. Если действительно льет дождь, то высказывание - истинное, а если солнечно, и бесполезно ждать дождя, то высказывание "Идет дождь" будет ложным.

Пример “ 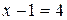” – не высказывание (неизвестно, какие значения принимает ).

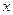“Студент второго курса” не высказывание

Ø Определение Элементарные высказывания не могут быть выражены через другие высказывания.

Ø Определение Составные высказывания –высказывания, которые можно выразить с помощью элементарных высказываний.

 

Пример “Число 22 четное” – элементарное высказывание.

Существуют два основных подхода к установлению истинности высказываний: эмпирический (опытный) и логический.

При эмпирическом подходе истинность высказывания устанавливается с помощью наблюдений, измерений, проведением экспериментов.

Логический подход заключается в том, что истинность высказывания устанавливается на основе истинности других высказываний, то есть без обращения к фактам, к их содержанию, то есть формально. Такой подход основан на выявлении и использовании логических связей между высказываниями, входящими в рассуждение.

 

2.2 Логика высказываний

 

Прежде всего нужно определиться с понятиями, потому что один и тот же раздел часто называют по-разному: математическая логика, логика высказываний (предложений), символическая логика, двузначная логика, пропозициональная логика, булева алгебра...

Ø Определение Логика высказываний - раздел логики, в котором вопрос об истинности или ложности высказываний рассматривается и решается на основе изучения способа построения высказываний из э лементарных (далее не разлагаемых и не анализируемых) высказываний с помощью логических операций конъюнкции ("и"), дизъюнкции ("или"), отрицания ("не"), импликации ("если..., то...") и др.

Ø Определение Исчисление высказываний – это аксиоматическая логическая система, интерпретацией которой является алгебра высказываний.

Наибольший интерес представляет построение формальной системы, которая среди всех возможных высказываний выделяет такие, которые являются логическими законами (правильно построенными рассуждениями, логическими умозаключениями, тавтологиями, общезначимыми высказываниями).

Формальные теории, не пользуясь естественным (разговорным) языком, нуждаются в собственном формальном языке, на котором записываются встречающиеся в нем выражения.

Ø Определение Формальная система, порождающая высказывания, которые являются тавтологиями и только их, называются исчислением высказываний (ИВ).

Формальная система ИВ определяется:

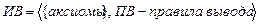
Какие символы лучше использовать для обозначения логических связок?

Остановимся на следующих обозначениях: отрицание, конъюнкция, дизъюнкция, импликация и эквивалентность. Обычно логические значения результатов применения связок записываются в виде таблиц (т.н. таблицы истинности).

 

2.3Логические связки..................................................

 

В естественном языке роль связок при составлении сложных предложений из простых играют следующие грамматические средства:

союзы «и», «или», «не»;

слова «если …, то», «либо … либо»,

«тогда и только тогда, когда» и др.

В логике высказываний логические связки, используемые для составления сложных высказываний, обязаны быть определены точно.

Рассмотрим логические связки (операции) над высказываниями, при которых истинностные значения составных высказываний определяются только истинностными значениями составляющих высказываний, а не их смыслом.

Широко употребительных логических связок пять.

отрицание (изображается знаком),

конъюнкция (знак ),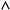

дизъюнкция (знак v),

импликация (знак )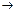

эквивалентность (знак ).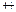

Ø Определение Отрицание высказывания P - высказывание, истинное тогда и только тогда, когда высказывание P ложно.

Ø Определение Конъюнкция двух высказываний P и Q - высказывание, истинное тогда и только тогда, когда истинны оба высказывания.

Ø Определение Дизъюнкция двух высказываний P и Q - высказывание, ложное тогда и только тогда, когда оба высказывания ложны.

Ø Определение Импликация двух высказываний P и Q - высказывание, ложное тогда и только тогда, когда P - истинно, а Q - ложно. Высказывание P называется посылкой импликации, а высказывание Q - заключением импликации.

Ø Определение Эквивалентность двух высказываний P и Q - высказывание, истинное тогда и только тогда, когда истинностные значения P и Q совпадают.

Употребление слов «если...» «то...» в алгебре логики отличается от употребления их в обыденной речи, где, как правило, считаем, что, если высказывание х ложно, то высказывание «Если х, то у» вообще не имеет смысла. Кроме того, строя предложение вида «если х, то у» в обыденной речи, всегда подразумеваем, что предложение у вытекает из предложения х. Употребление слов «если, то» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается.

 

2.4Логические операции

 

Основой цифровой техники служат три логические операции, лежащие в основе всех выводов компьютера. Это три логические операции: И, ИЛИ, НЕ, которые называют «тремя китами машинной логики».

К высказываниям можно применять известные из курса дискретной математики логические связки или логические операции. При этом получаются формулы. Формулы становятся высказываниями при подстановке всех значений букв.

Таблицы истинности основных логических операций.

 

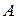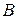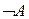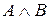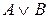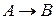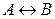Несколько переменных, связанных между собой с помощью логических операций, называют логической функцией.

Описание всякого исчисления включает в себя описание символов этого исчисления (алфавита), формул, являющихся конечными конфигурациями символов, и определение выводимых формул.

 

2.5 Алфавит исчисления высказываний

 

Алфавит исчисления высказывания состоит из символов трех категорий:

1. Символы первой категории: 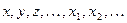Эти символы будем называть переменными высказываниями.

2. Символы второй категории: 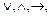они носят общее название логических связок.

Первый из них – знак дизъюнкции или логического сложения, второй – знак конъюнкции или логического умножения, третий – знак импликации или логического следования и четвертый – знак отрицания.

3. Третью категорию составляет пара символов (), называемая скобками.

Других символов исчисление высказываний не имеет

 

2.6 Формулы.Тавтология

Формулы исчисления высказываний представляют собой последовательности символов алфавита исчисления высказываний.

Для обозначения формул используются большие буквы латинского алфавита. Эти буквы не являются символами исчисления. Они представляют собой только условные обозначения формул.

Ø Определение Формула– правильно построенная составное высказывание:

1) Всякая буква есть формула.

2) Если 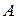, 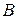- формулы, то формулами являются также , , , , .

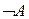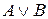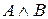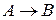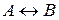Очевидно, не являются формулами слова: 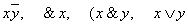) (в третьем из этих слов содержится не закрытая скобка, а в четвертом – нет скобок).

Заметим, что здесь никак не конкретизируются понятия логических связок. Обычно в запись формул вводят некоторые упрощения. Например, в записи формул опускаются скобки по тем же правилам, что и в алгебре высказываний.

Ø Определение. Формула называется тавтологией, если она принимает только истинные значения при любых значениях букв.

Ø Определение Формула ложная при любых значениях букв называется противоречием

Ø Определение Формула называется выполнимой, если на некотором наборе распределения истинностных значений переменных она принимает значение И.

Ø Определение Формула называется опровержимой, если при некотором распределении истинностных значений переменных она принимает значение Л.

Пример 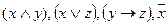являются формулами согласно п.2 определения.

По этой же причине будут формулами слова: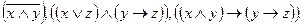

Одновременно с понятием формулы вводится понятие подформулы или части формулы.

1. Подформулой элементарной формулы является она сама.

2. Если формула имеет вид 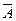, то ее подформулами являются: она сама, формула А и все подформулы формулы А.

3. Если формула имеет вид (А*В) (здесь и в дальнейшем под символом * будем понимать любой из трех символов 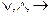), то ее подформулами являются: она сама, формулы А и В и все подформулы формул А и В.

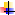Пример Для формулы 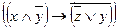ее подформулами будут:

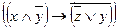- подформула нулевой глубины,

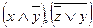-подформулы первой глубины,

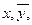
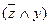-подформулы второй глубины,

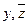-подформулы третьей глубины,

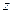-подформула четвертой глубины.

Таким образом, по мере “погружения вглубь структуры формулы” выделяем подформулы все большей глубины

Из курса дискретной математики известны основные логические эквивалентности (равносильности), которые являются примерами тавтологий. Все логические законы должны быть тавтологиями.

Иногда законы называются правилами вывода, которые определяют правильный вывод из посылок.

 

2.7Законы логики высказываний

 

Алгебра логики обладает коммутативными и ассоциативными законами относительно операций конъюнкции и дизъюнкции и дистрибутивным законом конъюнкции относительно дизъюнкции, эти же законы имеют место и в алгебре чисел.

Поэтому над формулами алгебры логики можно производить те же преобразования, которые проводятся в алгебре чисел (раскрытие скобок, заключение в скобки, вынесение за скобки общего множителя).

Рассмотрим основные законы логики высказываний.

 

 

1. Коммутативность:

, .

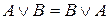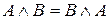2. Ассоциативность:

, .

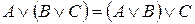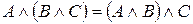3. Дистрибутивность:

, .

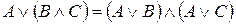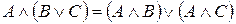4. Идемпотентность: , .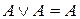

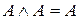5. Закон двойного отрицания: .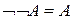

6. Закон исключения третьего: .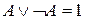

7. Закон противоречия: .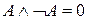

8. Законы де Моргана:

, .

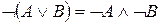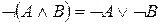9. Законы идемпотентности (свойства операций с логическими константами)

В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых ”сомножителей” равносильна одному из них

, , , .

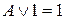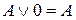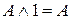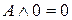Здесь 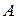, 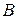и 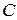– любые буквы.

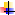Примеры. формула 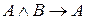тавтология.

2. 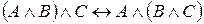тавтологией.

3. 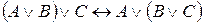тавтологией.

v Теорема. Пусть формулы 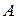и 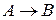– тавтологии. Тогда формула 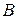– тавтология.

v Теорема. Пусть формула 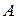– тавтология, 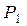, , 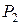…, 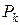– буквы в формуле 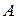, , 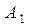, 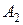…, 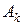– любые формулы. Тогда новая формула 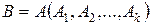– тавтология.

 

 

2.8 Формальные теории. Выводимость. Интерпретация

 

Ø Определение Формальная теория считается заданной, если известны следующие четыре составляющих:

1. Алфавит – конечное или счетное множество символов.

2. Формулы,которые по специальным правилам строятся из символов алфавита.

3. Аксиомы

4. Правила вывода – множество отношений, позволяющие из аксиом получать теоремы формальной теории.

Ø Определение Вывод формальной теории - последовательность формул 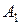, , 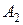…, , 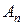в которой все формулы – либо аксиомы, либо получаются из предыдущих по правилам вывода.

Ø Определение Формула 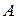выводима из множества формул 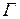( 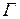├ 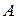), если существует вывод 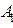, , 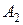…, , 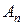где 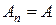, и есть три возможности: 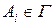; 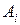- аксиома; 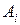получаются из предыдущих формул по правилам вывода. Формулы из множества 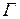называются посылками или гипотезами вывода.

Ø Определение Интерпретацией множества формул 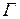называется область интерпретации 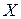и заданное на ней соответствие, которое каждой предикатной букве 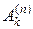ставит в соответствие 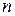-местный предикат на 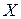, каждой функциональной букве 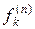– 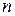-местную функцию на 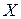, каждой предметной константе 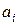– элемент множества .

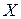При интерпретации формулы превращаются в предикаты на множестве .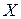

Если формула не имеет свободных переменных, то после интерпретации она превращается в высказывание.

Ø Определение. Формула называется общезначимой, если она истинна в любой интерпретации.