Пусть А – доказуемая формула; 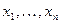 - переменные, а
- переменные, а 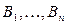 - любые формулы ИВ. Тогда результат одновременной подстановки в формулу А вместо
- любые формулы ИВ. Тогда результат одновременной подстановки в формулу А вместо 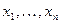 соответственно формул
соответственно формул 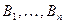 является доказуемой формулой.
является доказуемой формулой.
Схематично операция СПП записывается так:
├А______
├ 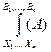
Так, в рассмотренном выше примере вместо шагов 4-5-6 и 9-10-11 можно было сразу применить СПП и тогда вместо 12 получим желаемый результат за 8 ходов:
1) 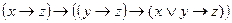 ....(
....(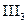 ) (1)
) (1)
2) 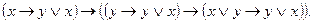 ... (2)
... (2)
3) 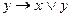 ...(
...(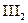 ) (3)
) (3)
4) 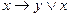 ...
... 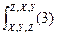 (4)
(4)
5) 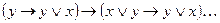 (2),(4), ПЗ (5)
(2),(4), ПЗ (5)
6) 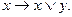 ... (
... (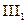 ) (6)
) (6)
7) 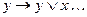
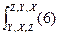 (7)
(7)
8) 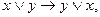 ... (5), (7), ПЗ (8)
... (5), (7), ПЗ (8)
Правило сложного заключения.
Правило сложного заключения также допускает обобщение.
Второе производное правило, получаемое в результате такого обобщения, применяется к формулам вида
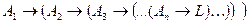
и формулируется так:
Если формулы 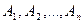 и
и 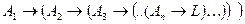 доказуемы, то и формула L доказуема.
доказуемы, то и формула L доказуема.
Правило сложного заключения схематично записывается так:
├А1, ├А2, …,├Аn, ├A1→(A2→(A3→(...(An→L) …)))
├ L
Следующие правила знакомы по тождественно истинным формулам алгебры логики, носящим те же наименования.
Правило силлогизма.
Если доказуемы формулы А→В и В→С, то доказуема формула А→С, т. е.
├А→В,├В→С
├А→С
Правило контр позиции.
Если доказуема формула А→В, то доказуема формула 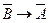 , т. е.
, т. е.
├ А →В
├ 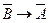
На примере этого правила покажем, как доказываются такие утверждения в исчислении высказываний. Сделаем одновременную подстановку 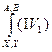 , получим доказуемую формулу ├(А→В)→├(
, получим доказуемую формулу ├(А→В)→├(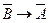 ). (1)
). (1)
Но по условию доказуема формула ├А→В. (2)
Из формул (2) и (1) по правилу заключения имеем ├ 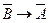 .
.
 2017-11-01
2017-11-01 911
911








