Доказательство некоторых законов логики

Правила выводимости, и особенно теорема дедукции, позволяют доказать ряд законов логики.

1. Закон перестановки посылок.

├(x→(y→z)) →(y→(x→z)). (1)

Доказательство:

Можно показать, что из совокупности формул Н={x→(y→ z), y, x} следует вывод x→(y→ z), y, x, y→ z, z, т. е. из совокупности Н выводима формула z.

Тогда по обобщенной теореме дедукции доказуема формула (1). И тогда по ПЗ из закона перестановки посылок вытекает правило перестановки посылок в доказуемых формулах: ├(x→(y→ z))

├(y→(x→ z)). (2)

Действительно, если ├x→(y→ z), (2), то из (1) и (2) по правилу заключения следует ├y→(x→z).

2. Закон соединения посылок

├(x→(y→ z)) →( →z). (3)

Доказательство:

Можно показать, что из совокупности формул Н={x→(y→ z), } следует вывод x→(y→ z), , → х, → y, x, y, y→ z, z, т. е. из совокупности Н выводима формула z. Тогда по обобщенной теореме дедукции доказуема формула (3).

Из закона соединения посылок вытекает правило соединения посылок в доказуемых формулах: ├(x→(y→z))

├ →z. (4)

Действительно, если ├x→(y→z), (4), то из (3) и (4) по правилу заключения следует ├ →z.

3. Закон разъединения посылок.

├( →z) →(x→(y→z)). (5)

Так как из совокупности формул Н={x, y, →z} следует вывод x, y, →z, , z, то из совокупности формул Н выводима формула z. Тогда по обобщенной теореме дедукции доказуема формула (5).

Из закона разъединения посылок вытекает правилоразъединения посылок в доказуемых формулах: ├ → z

├х→(y→z). (6)

Действительно, если ├ →z)), (6), то из (5) и (6) по правилу заключения следует

├х→(y→z).

4. ├х→(). (7)

Доказательство:

Сделаем подстановки в аксиомы и : и .

В результате получим доказуемые формулы:

├х→(), (8) и ├ . (9)

Из формул (8)и (9)по правилу силлогизма следует: ├ .

Используя закон соединения посылок, получим: ├ .

Используя правило снятия двойного отрицания, получим: ├ .

И, наконец, применяя закон разъединения посылок, получим (7).

5. Закон исключенного третьего: ├ .

Доказательство:

Воспользуемся доказуемой формулой ├ (10)

и, сделав в ней подстановку , получим:

├ . (11)

Также сделаем подстановку в формуле (7), заменяя 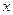на , а y на :

├ (). (12)

Используя закон соединения посылок, будем иметь: ├ . (13)

Из формул (11) и (13) по правилу силлогизма получаем ├ . (14)

Из формулы (14) по правилу контрапозиции следует├ .

Используя оба правила снятия двойного отрицания, получаем ├ (15)

Пусть теперь y- любая доказуемая формула R, тогда из формул ├R, ├R по правилу заключения получаем ├ .

6. ├ . Примем этот закон без доказательства.

2.14 Связь между алгеброй и исчислением высказываний

Формулы исчисления высказываний можно интерпретировать как формулы алгебры высказываний. Для этого будем трактовать переменные исчисления высказываний как переменные алгебры высказываний, т. е. переменные в содержательном смысле, принимающие два значения: истина и ложь (1 и 0).

Операции определим так же, как в алгебре высказываний.

При этом всякая формула исчисления высказываний при любых входящих в нее переменных будет принимать одно из значений 1 или 0, вычисляемое по правилам алгебры высказываний.

Введем понятие значения формулы исчисления высказываний. Пусть А- формула исчисления высказываний, х₁,х₂,…,х_n- попарно различные переменные, среди которых находятся все переменные, входящие в формулу А. Обозначим через а₁, а₂,…,а_n набор значений этих переменных, состоящих из 1 и 0, длины n. Очевидно, что вектор (а₁, а₂,…,а_n) имеет 2ⁿ значений.

Имеют место три теоремы, которые устанавливают связь между основными фактами алгебры высказываний и исчисления высказываний.

v Теорема 1. Каждая формула, доказуемая в исчислении высказываний, является тождественно истинной в алгебре высказываний.

Формулировка этой теоремы содержит в себе три положения:

1)Каждая аксиома исчисления высказываний – тождественно истинная формула в алгебре высказываний.

2)Правило подстановки, примененное к тождественно истинным формулам, приводит к тождественно истинным формулам.

3)Правило заключения, примененное к тождественно истинным формулам, приводит к тождественно истинным формулам.

v Теорема 2. (о выводимости) Пусть А –некоторая формула исчисления высказываний; х₁,х₂,…,х_{n –} набор переменных, содержащих все переменные, входящие в формулу А; а₁, а₂,…,а_n – произвольный фиксированный набор значений этих переменных. Обозначим через Н конечную совокупность формул

, где

Тогда:

1) Если R_a1,a2,..,an(A)=1, то H├A.

2) Если R_a1,a2,..,an(A)=0, то H├ 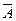, где R_a1,a2,..,an(A)–значение формулы А на наборе а₁, а₂,…,а_n.

v Теорема 3 Каждая тождественно истинная формула алгебры высказываний доказуема в исчислении высказываний.