Понятие выводимости формул из совокупности формул

 

Будем рассматривать конечную совокупность формул Н={А₁,А₂,…,А_n}.

Ø Определение формулы, выводимой из совокупности Н.

1)Всякая формула А_i ,является формулой, выводимой из Н.

2) Всякая доказуемая формула выводима из Н.

3) Если формулы С и С→В выводимы из совокупности Н, то формула В также выводима из Н.

Если некоторая формула В выводима из совокупности Н, то это записывают так: Н├В.

Нетрудно видеть, что класс формул, выводимых из совокупности Н, совпадает с классом доказуемых формул в случае, когда совокупность Н содержит только доказуемые формулы, и в случае, когда Н пуста. Если же совокупность формул Н содержит хотя бы одну не доказуемую формулу, то класс формул, выводимых из Н, шире класса доказуемых формул.

Пример. Доказать, что из совокупности формул Н={А,В} выводима формула .

Так как А и В , то по определению выводимой формулы

Н├А, (1)

Н├В. (2)

Возьмем аксиомы и , и выполним подстановки и .

В результате получим доказуемые формулы, которые выводимы из Н по определению выводимой формулы, т. е.

Н├(А→А)→((А→В)→(А )), (3)

Н├В→(А→В), (4)

Так как формула А→А доказуема, то Н├А→А. (5)

Из формул (5) и (3) по правилу заключения получаем: Н├(А→В)→(А )). (6)

Из формулы (2) и (4) по правилу заключения получаем: Н├А→В. (7)

Из формул (7) и (6) по правилу заключения получаем: Н├А . (8)

И, наконец, из формул (1) и (8) получаем:

Н├ (9)

При доказательстве выводимости формулы из совокупности формул можно пользоваться не только основным правилом заключения, но и правилом сложного заключения.

Тогда, пользуясь этим правилом, предложение (9) можно получить из предложений (5), (7), (1) и (3).

Понятие вывода

Ø Определение Выводом из конечной совокупности формул Н называется всякая конечная последовательность формул В₁,В₂,…,В_к, всякий член которой удовлетворяет одному из следующих трех условий:

1) он является одной из формул совокупности Н,

2) он является доказуемой формулой,

3) он получается по правилу заключения из двух любых предшествующих членов последовательности В₁,В₂,…,В_к.

Как было показано в предыдущем примере_, выводом из совокупности формул Н={А,В} является конечная последовательность формул:

А, В, (А→А)→((А→В)→(А )), (А→В), А→А, (А→В)→(А )), А→В, А , . (см. формулы 1,2,3,7,5,6,8).

Если же здесь воспользоваться правилом сложного заключения, то вывод можно записать так:

А, В, (А→А)→((А→В)→(А )), В→(А→В), А→А, А→В, . (см. формулы 5, 7, 1, 3).

Из определения выводимой формулы и вывода из совокупности формул следуют очевидные свойства вывода:

Свойства вывода

1)Всякий начальный отрезок вывода из совокупности Н есть вывод из Н.

2)Если между двумя соседними членами вывода из Н (или в начале или в конце его) вставить некоторый вывод из Н, то полученная новая последовательность формул будет также выводом из Н.

3)Всякий член вывода из совокупности Н является формулой, выводимой из Н.

Всякий вывод из Н является выводом его последней формулы.

4)Если (включено), то всякий вывод из Н является выводом из W.

5)Для того, чтобы формула В была выводима из совокупности Н, необходимо и достаточно, чтобы существовал вывод этой формулы из Н.

 

Правила выводимости

Эти правила непосредственно следуют из свойств вывода с использованием ПП и ПЗ.

Пусть Н и W – две совокупности формул исчисления высказываний. Будем обозначать через Н, W их объединение, т. е. Н,W= .

В частности, если совокупность W состоит из одной формулы С, то будем записывать объединение в виде Н,С.

 

 

Основные правила выводимости:

1. H ├ A Это правило следует непосредственно из определения вывода

2. H,C ├ A,H├C

3. H,C ├ A, W├C

4. H ├ C→A

H├C→A

В частности, если , то если C├ A C→A

5A. Обобщенная теорема дедукции: {C₁, C₁, …, C_k}├ A

├C₁ →(C₂→(C₃→…(C_k→A)…))

Теорема. (обратная теорема дедукции.)

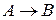
H├ H, ├ .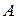

 

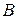6. Правило введения конъюнкции: H├A,H├B

H├

7. Правило введения дизъюнкции: H,A├C;Н,B├C.

H, ├C

 

 

2.13 Построение вывода в логике высказываний

Пример

Докажем, что выводима формула ├ .

Док-во

По теореме, обратной теореме дедукции, посылку можно перенести в левую часть:

├ .

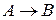Проделаем эту операцию еще раз:

, ├ .

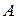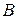1. – гипотеза.

2. 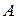– гипотеза.

Формулу 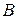удобно получить из аксиомы А3.

Поэтому запишем эту аксиому:

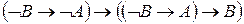
К формулам 1 и 3 применим правило вывода Modus ponens

4. 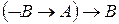. МР 1, 3.

Посылку в формуле 4 можно получить из аксиомы А1, если заменить 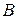на :

5. . А1 с подстановкой вместо – .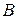

Далее дважды применяем правило Modus ponens:

6. . МР 2, 5.

7. 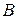. МР 6, 4.

Вывод построен, и применением теоремы дедукции мы доказали выводимость первоначальной формулы.

Отметим, что вывод может быть неединственным, в частности, формулы могут быть записаны в другом порядке.