1. Умножение матрицы на число.
Произведением матрицы  на число
на число 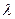 называется матрица
называется матрица 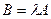 , каждый элемент которой равен произведению соответствующего элемента матрицы
, каждый элемент которой равен произведению соответствующего элемента матрицы  на число
на число 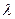 , т.е.
, т.е. 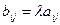 для
для 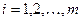 ;
; 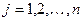 .
.
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е 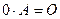 .
.
2. Сложение матриц.
Суммой двух матриц  и
и  одинакового размера
одинакового размера 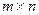 называется матрица
называется матрица 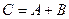 , каждый элемент которой
, каждый элемент которой 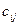 равен сумме соответствующих элементов матриц
равен сумме соответствующих элементов матриц  и
и  , т.е.
, т.е. 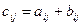 для
для 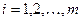 ;
; 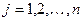 (т.е. матрицы складываются поэлементно).
(т.е. матрицы складываются поэлементно).
3. Вычитание матриц.
Разность двух матриц одинакового размера определяется через предыдущие операции: 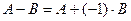 .
.
Умножение матриц.
Произведение матриц  и
и  определено, когда число столбцов матрицы
определено, когда число столбцов матрицы  равно числу матрицы
равно числу матрицы  . Произведением матриц
. Произведением матриц 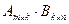 называетсятакая матрица
называетсятакая матрица 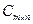 , каждый элемент которой
, каждый элемент которой 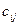 равен суммепроизведений элементов
равен суммепроизведений элементов 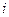 -й строки матрицы
-й строки матрицы  на соответствующие элементы
на соответствующие элементы  -го столбца матрицы
-го столбца матрицы  :
: 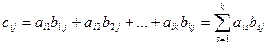 ,
, 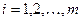 ;
; 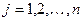 .
.
(Иными словами, матрицы умножаются строка на столбец).
Операции над матрицами обладают следующими свойствами:
1) 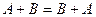 ;
;
2)  ;
;
3) 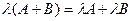 .
.
4) 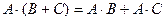 ;
;
5) 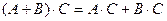 ;
;
6) 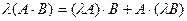 ;
;
7) 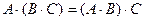 .
.
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а) Если произведение матриц 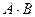 существует, то после перестановки сомножителей местами произведения матриц
существует, то после перестановки сомножителей местами произведения матриц 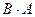 может и не существовать.
может и не существовать.
б) Если даже произведения 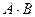 и
и 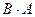 существуют, то они могут быть матрицами разных размеров.
существуют, то они могут быть матрицами разных размеров.
в) В случае, когда оба произведения 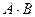 и
и 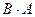 существуют и оба - матрицы одинакового размера (это возможно только при умножении квадратных матриц
существуют и оба - матрицы одинакового размера (это возможно только при умножении квадратных матриц  и
и  одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е.
одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е.  .
.
В частном случае коммутативным законом обладает произведение любой квадратной матрицы 
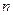 -го порядка на единичную матрицу
-го порядка на единичную матрицу 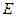 того же порядка, причем это произведение равно
того же порядка, причем это произведение равно  :
: 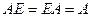
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 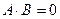 , не следует, что
, не следует, что 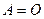 или
или 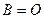 .
.
5. Возведение в степень. Целой положительной степенью квадратной матрицы  называется произведение
называется произведение 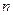 матриц, равных
матриц, равных  , т.е.
, т.е.
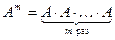 .
.
Заметим, что операция возведения в степень определена только для квадратных матриц. Полагают 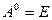 ,
, 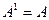 . Нетрудно показать, что
. Нетрудно показать, что 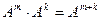 ,
, 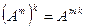 . Если
. Если 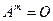 , то это не означает, что матрица
, то это не означает, что матрица 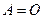 .
.
6. Транспонирование матрицы - переход от матрицы  к матрице
к матрице 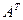 , в которой строки и столбцы поменяны местами с сохранением порядка. Матрица
, в которой строки и столбцы поменяны местами с сохранением порядка. Матрица 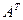 называется транспонированной относительно матрицы
называется транспонированной относительно матрицы  :
:
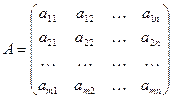 ,
, 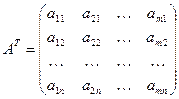 . (2)
. (2)
Из определения следует, что если матрица  имеет размер
имеет размер 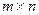 , то транспонированная матрица
, то транспонированная матрица 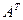 имеет размер
имеет размер 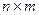 .
.
Свойства операции транспонирования:
1) 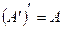
2) 
3) 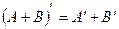
4)  .
.
 2017-11-01
2017-11-01 330
330








