2017-11-01
607
Определитель квадратной матрицы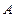 
– это число, характеризующего эту матрицу. Он обозначается 
или 
.
Определителем матрицы первого порядка 
, или определителем первого порядка, называется число, определяемое по формуле: 
.
Например, пусть 
, тогда 
.
Определителем матрицы второго порядка 
, или определителем второго порядка, называется число, которое вычисляется по формуле:
(3).
Произведения 
и 
называются членами определителя второго порядка.
Пусть дана квадратная матрица третьего порядка:
.
Определителем матрицы 
третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
(4).
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (4), легко запомнить, пользуясь схемой (рис. 1), которая называется правилом Сарруса.
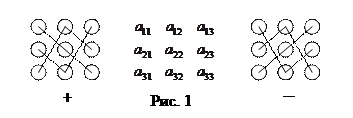
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия.
Рассмотрим квадратную матрицу n-го порядка:
.
Из общего числа 
элементов этой матрицы выберем набор, содержащий n элементов, таким образом, чтобы в него входило по одному элементу из каждой строки и каждого столбца. Например, наборы элементов 
или 
соответствуют главной и побочной диагоналям матрицы.
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.
. (5)
Номера столбцов 
образуют при этом перестановку J из n чисел: 1, 2,..., n. Всего существует 
различных перестановок из n.
Введем понятие беспорядка, или инверсии, в перестановке J. Это наличие пары чисел, в которой большее число предшествует меньшему. Например, в перестановке из трех чисел J =(2; 1; 3) имеется одна инверсия (2; 1), а в перестановке J =(3; 2; 1) - три: (3; 2), (3; 1), (2; 1). Обозначим через r(J) количество инверсий в перестановке J.
Возвращаясь к наборам (5) из элементов матрицы А, мы можем каждому такому набору поставить в соответствие произведение его элементов:
. (6)
и число r(J), равное количеству инверсий в перестановке из номеров соответствующих столбцов.
Определителемквадратной матрицы п-го порядка, или определителем п-го порядка, называется число, равное алгебраической сумме членов, каждый из которых является произведением п элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как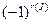 
где r(J) - число инверсий в перестановке J из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания:
(7)
где сумма берется по всем перестановкам J.
Заметим, что с ростом n резко увеличивается число членов определителя (), поэтому даже для n = 4 использование формулы (7) весьма трудоемко (получим 24 слагаемых).
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
Пусть дана квадратная матрица А n -го порядка.
Минором 
элемента 
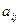матрицы n -го порядка называется определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i -й строки и j- гo столбца.
Каждая матрица n -го порядка имеет миноров (n-1)-го порядка. Алгебраическим дополнением 
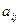элемента матрицы n -го порядка называется его минор, взятый со знаком 
:
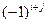, (8)
т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (i+j) - четное число, и отличается от минора знаком, когда (i+j) - нечетное число.
Для вычисления определителей квадратных матриц удобно пользоваться следующей теоремой:
Теорема Лапласа (частный случай). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(9)
(разложение по элементам i -й строки; i = 1,2,… n;
(10)
(разложение по элементам j -го столбца; j =1,2,..., n).
Таким образом, применение теоремы Лапласа позволяет свести вычисление определителей n- гопорядка к вычислению более простых определителей (n- 1)-го порядка.
