Рассмотрим некоторые линейные преобразования дифференциала
 ;
;
 ;
;
 .
.
Дифференциал аргумента на измениться, если к аргументу прибавить постоянное число, то есть
 .
.
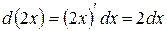 ,
, 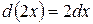 ;
;
 ,
, 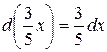 ;
;
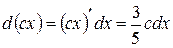 , где
, где 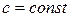 .
.
Постоянный множитель можно выносить за знак дифференциала и вносить под знак дифференциала.
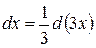 ;
;
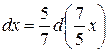 .
.
При умножении аргумента, стоящего под знаком дифференциала, на постоянное число, дифференциал изменяется во столько же раз, что и постоянное число.
Чтобы величина дифференциала аргумента не изменилась, при умножении аргумента на  , где
, где 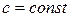 , необходимо сам дифференциал умножить на дробь, обратную
, необходимо сам дифференциал умножить на дробь, обратную  , то есть на
, то есть на 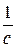
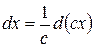 .
.
Пример 5. Найти 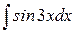 .
.
Решение
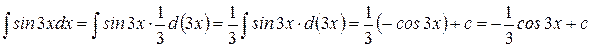 .
.
При решении применяли линейное преобразование дифференциала (3) и формулу интегрирования (6).
Пример 6. Найти 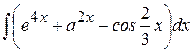 .
.
Решение
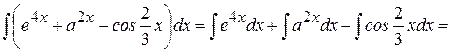
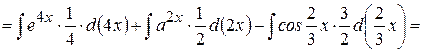

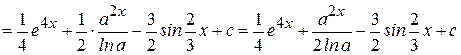 .
.
При решении применяли линейное преобразование дифференциала (3) и формулы интегрирования (4), (5), (7).
Пример 7. Найти 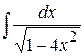 .
.
Решение
Этот интеграл приводится к табличному (10)
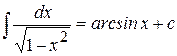 .
.
Выполним некоторые преобразования
 .
.
Пример 8. Найти 
Решение
Этот интеграл приводится к табличному
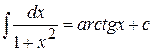 .
.
Выполним некоторые преобразования
Ошибка! Ошибка связи.
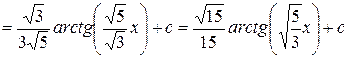 .
.
Мы разобрали простейшие примеры, в которых функции могли быть выражены путем несложных преобразовании в виде, позволяющим применить для нахождения интеграла основные табличные формулы.
Для закрепления этого способа необходимо решить следующие примеры
1) Найти 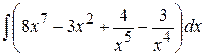 Ответ:
Ответ: 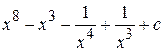
2) Найти 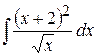 Ответ:
Ответ: 
3) Найти  Ответ:
Ответ: 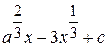
4) Найти 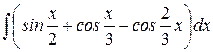 Ответ:
Ответ: 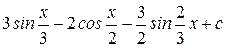
5) Найти 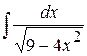 Ответ:
Ответ: 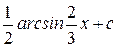
6) Найти 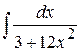 Ответ:
Ответ: 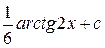
Второй способ – способ подстановки.
Если заданный интеграл простейшими преобразованиями трудно привести (или совсем нельзя привести) к табличному, то для его отыскания применяются особые приемы. Одним из них является интегрирование способом подстановки. В основе метода подстановки лежит введение новой переменной, затем дифференцирование этой постановки, замена в искомом интеграле всего через новую переменную, а только потом использование основных формул интегрирования. После того, как нашли интеграл, опять возвращаемся к старой переменной.
Пример 9. Найти  .
.
Решение
Положим,
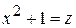 ,
,
где 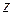 - новая переменная.
- новая переменная.
Возьмем дифференциал от обеих частей равенства
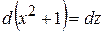 .
.
Получим
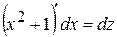 ,
,
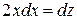 ,
,
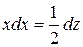 .
.
Заменив в искомом интеграле 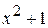 и
и  их найденными значениями и применив формулу (2)
их найденными значениями и применив формулу (2)
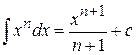
будем иметь
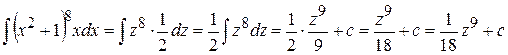 .
.
Но ответ должен быть представлен как функция от переменной  , поэтому, подставив вместо
, поэтому, подставив вместо 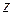 его значение из подстановки, получим
его значение из подстановки, получим
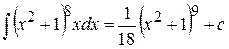 .
.
Пример 10. Найти  .
.
Решение
Введем подстановку
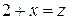 .
.
Продифференцируем равенство
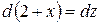 ,
,
получим
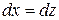 .
.
Подставим в подынтегральное выражение
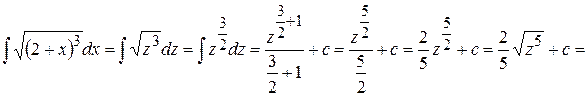
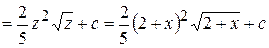 .
.
Пример 11. Найти  .
.
Решение
Обозначим
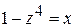 .
.
Продифференцируем
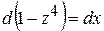 ,
,
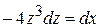 ,
,
 .
.
Подставив в подынтегральное выражение вместо  и
и 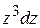 их значения, заменив корень степенью с дробными показателями, а затем, введя отрицательный показатель и применив формулу интеграл степени, получим
их значения, заменив корень степенью с дробными показателями, а затем, введя отрицательный показатель и применив формулу интеграл степени, получим
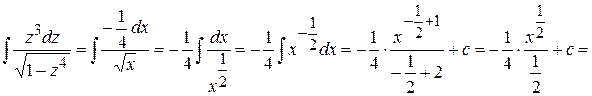
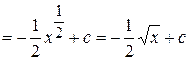 .
.
Перейдя к прежней переменной 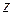 , получим
, получим
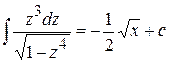 .
.
Пример 12. Найти 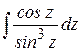 .
.
Решение можно записать короче
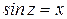 ,
,
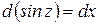 ,
,
 .
.
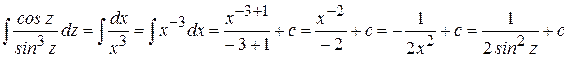 .
.
Пример 13. Найти 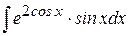 .
.
Решение
Положим
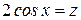 ,
,
продифференцируем
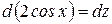 ,
,
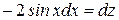 ,
,
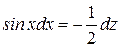 .
.
Заменив в искомом интеграле 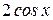 и
и 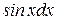 их найденными значениями и применив свойство (3) и формулу (4), получим
их найденными значениями и применив свойство (3) и формулу (4), получим
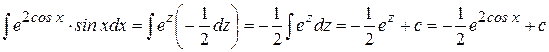 .
.
Пример 14. Найти 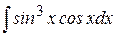
Решение
Вводим подстановку
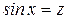 ,
,
продифференцируем это равенство
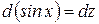 ,
,
 .
.
Поставим вместо 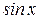 и
и 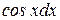 в искомый интеграл
в искомый интеграл
 .
.
Замечание. Если подынтегральное выражение содержит 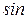 и
и  одного и того же аргумента, причем одна из функций входит в какой-либо степени, то через новую переменную обозначают первую степень той функции, которая входит в степени.
одного и того же аргумента, причем одна из функций входит в какой-либо степени, то через новую переменную обозначают первую степень той функции, которая входит в степени.
При решении способом подстановки важно правильно выбрать подстановку, а для этого недостаточно простого знания формул, нужен еще опыт, который накапливается постоянно в процессе решения примеров.
Нужно устно выбранную подстановку продифференцировать и посмотреть остальное выражение в подынтегральном выражении можно ли заменить через новую переменную. Если можно, то выбранную подстановку верно выбрали. Если нет, то нужна другая подстановка. Запись решения следует производить так:
Пример 15. 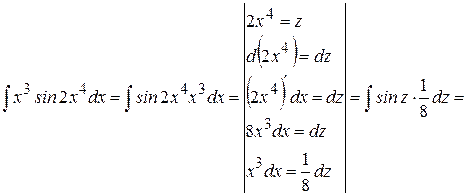
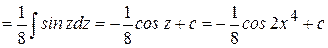 .
.
Пример 16. 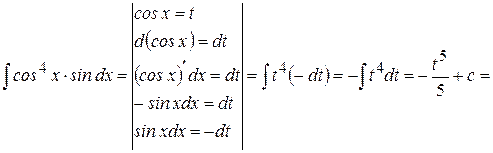
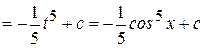 .
.
Пример 17. 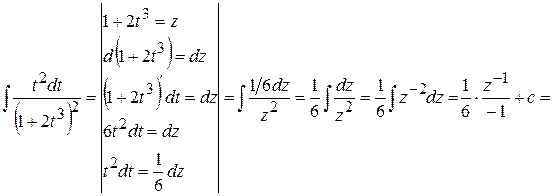
 .
.
Для закрепления интегрированием способом подстановки, необходимо решить следующие примеры:
Найти
1) 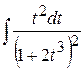 Ответ:
Ответ: 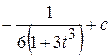 ;
;
2) 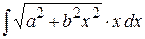 Ответ:
Ответ: 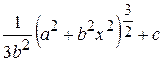 ;
;
3) 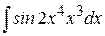 Ответ:
Ответ: 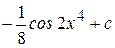 ;
;
4) 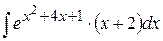 Ответ:
Ответ: 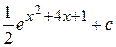 ;
;
5)  Ответ:
Ответ: 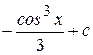 ;
;
6) 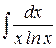 Ответ:
Ответ: 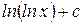 .
.
 2017-11-01
2017-11-01 930
930








